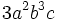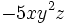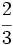Plantilla:Monomios
De Wikipedia
| Revisión de 07:16 7 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:18 7 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| |url1=https://www.youtube.com/watch?v=ziPklrOtsNk | |url1=https://www.youtube.com/watch?v=ziPklrOtsNk | ||
| }} | }} | ||
| + | {{wolfram desplegable|titulo=Grado de un monomio|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Grado de un monomio'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | Indica el grado y el coeficiente de los siguientes monomios: | ||
| + | |||
| + | :a) <math>3a^2b^3c\!</math> | ||
| + | :b) <math>-5xy^2z\!</math> | ||
| + | :c) <math>\cfrac{2}{3}</math> | ||
| {{p}} | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=degree 3a^2b^3c´}} | ||
| + | :b) {{consulta|texto=degree -5xy^2z}} | ||
| + | :b) {{consulta|texto=degree 2/3}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | |||
| ===Monomios semejantes=== | ===Monomios semejantes=== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 50: | Línea 73: | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_2a.htm | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_2a.htm | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Videotutoriales|titulo=Monomios semejantes|enunciado= | {{Videotutoriales|titulo=Monomios semejantes|enunciado= | ||
| {{Video_enlace_matefacil | {{Video_enlace_matefacil | ||
| Línea 79: | Línea 101: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{wolfram desplegable|titulo=Grado de un monomio|contenido= | ||
| - | {{wolfram | ||
| - | |titulo=Actividad: ''Grado de un monomio'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | Indica el grado y el coeficiente de los siguientes monomios: | ||
| - | |||
| - | :a) <math>3a^2b^3c\!</math> | ||
| - | :b) <math>-5xy^2z\!</math> | ||
| - | :c) <math>\cfrac{2}{3}</math> | ||
| - | {{p}} | ||
| - | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | |||
| - | :a) {{consulta|texto=degree 3a^2b^3c´}} | ||
| - | :b) {{consulta|texto=degree -5xy^2z}} | ||
| - | :b) {{consulta|texto=degree 2/3}} | ||
| - | |||
| - | {{widget generico}} | ||
| - | }} | ||
| - | }} | ||
| - | }} | ||
Revisión de 07:18 7 sep 2017
- Monomio es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas a potencias de exponente natural.
- Se llama coeficiente de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si el coeficiente es un 1 no suele escribirse. Si el coeficiente es 0, el monomio resultante es el número 0.
- Se denomina grado de un monomio a la suma de los exponentes de las letras. Si no hay letras el grado es cero.
- a)
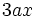 es un monomio de grado 2 y coeficiente 3.
es un monomio de grado 2 y coeficiente 3.
- b)
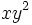 es un monomio de grado 3 y coeficiente 1.
es un monomio de grado 3 y coeficiente 1.
- c)
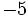 es un monomio de grado 0 y coeficiente -5.
es un monomio de grado 0 y coeficiente -5.
- d) En la siguiente escena se puede observar el coeficiente y el grado de un monomio. En la parte superior se pueden cambiar los exponentes de las letras a, b, y x. Para cambiar el coeficiente del monomio modifica la casilla de abajo.
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio.
Aprende a calcular el grado relativo y absoluto de un monomio.
Nota: Al "grado absoluto" de un monomio se le llama simplemente "grado" del monomio.
Monomios semejantes
Son monomios semejantes aquellos en los que aparecen las mismas letras con los mismos exponentes.
Son monomios semejantes: 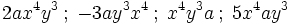
Las letras pueden aparecer en distinto orden ya que por la propiedad conmutativa las podemos reordenar.
Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio. También practicaras con monomios semejantes y opuestos.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Aprende a distiguir cuando dos monomios son o no semejantes.
Encuentra los términos semejantes.