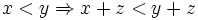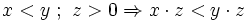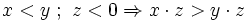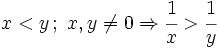Plantilla:Reglas desigualdades
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:26 16 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Teorema_sin_demo|titulo=Reglas para trabajar con desigualdades|enunciado= | {{Teorema_sin_demo|titulo=Reglas para trabajar con desigualdades|enunciado= | ||
| - | :Sean <math> x, y, z \in \mathbb{R}</math>, se cumplen las siguientes propiedades: | + | Sean <math> x, y, z \in \mathbb{R}</math>, se cumplen las siguientes propiedades: |
| - | #{{b4}}<math> x<y \Rightarrow x+z<y+z </math> | + | {{p}} |
| - | #{{b4}}<math> x<y~,~ z>0 \Rightarrow xz<yz </math> | + | :'''1.'''{{b}} <math> x<y \Rightarrow x+z<y+z </math> |
| - | #{{b4}}<math> x<y~,~ z<0 \Rightarrow xz>yz </math> | + | |
| - | #{{b4}}<math> x<y \Rightarrow \cfrac{1}{x} > \cfrac{1}{y} </math> | + | :'''2.'''{{b}} <math> x<y~;~ z>0 \Rightarrow x \cdot z<y \cdot z </math> |
| + | |||
| + | :'''3.'''{{b}} <math> x<y~;~ z<0 \Rightarrow x \cdot z>y \cdot z </math> | ||
| + | |||
| + | :'''4.'''{{b}} <math> x<y \, ; \ x,y \ne 0 \Rightarrow \cfrac{1}{x} > \cfrac{1}{y} </math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | Como consecuencia, en una inecuación: | ||
| + | *Lo que está sumando en un lado de la desigualdad, pasa restando al otro miembro sin afectar a la desigualdad. Y viceversa. | ||
| + | *Lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. En este caso la desigualdad sólo cambia de sentido si el número que pasa multiplicando o dividiendo es negativo. | ||
| + | {{p}} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=¿Cuándo debe cambiar de sentido una desigualdad? | ||
| + | |duracion=10'00" | ||
| + | |sinopsis= ¿Cuándo debe cambiar de sentido una desigualdad?. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=-xd3IY4ur-o&index=4&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | ||
| }} | }} | ||
Revisión actual
Como consecuencia, en una inecuación:
- Lo que está sumando en un lado de la desigualdad, pasa restando al otro miembro sin afectar a la desigualdad. Y viceversa.
- Lo que está multiplicando a todo un miembro, pasa dividiendo al otro miembro. Y viceversa. En este caso la desigualdad sólo cambia de sentido si el número que pasa multiplicando o dividiendo es negativo.
¿Cuándo debe cambiar de sentido una desigualdad?. Ejemplos.
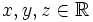 , se cumplen las siguientes propiedades:
, se cumplen las siguientes propiedades: