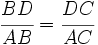Plantilla:Aplicaciones de los criterios de semejanza
De Wikipedia
| Revisión de 16:15 24 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas. | Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas. | ||
| {{p}} | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Aplicaciones de los criterios de semejanza | ||
| + | |descripcion=Ejercicios de aplicación de los criterios de semejanza de triángulos: | ||
| + | *Medición de alturas con sombras. | ||
| + | *Medición de alturas con espejos. | ||
| + | *¿Cómo pudo medir Tales la altura de una pirámide? | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena7/2quincena7_contenidos_2c.htm | ||
| + | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica. | |descripcion=En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica. | ||
| Línea 11: | Línea 19: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Aplicaciones de los criterios de semejanza (Ampliación)|enunciado= | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Teorema de la bisectriz | |titulo1=Teorema de la bisectriz | ||
| Línea 35: | Línea 44: | ||
| '''Problema:''' | '''Problema:''' | ||
| - | En un triángulo ABC se traza la mediana CM y desde A se traza la mediana AN que corta a la mediana CM en su punto medio T. Sabiendo que TN = 5 cm, calcula el valor de AT. | + | En un triángulo ABC se traza la mediana CM y desde A se traza el segmento AN que corta a la mediana CM en su punto medio T. Sabiendo que TN = 5 cm, calcula el valor de AT. |
| Línea 51: | Línea 60: | ||
| }} | }} | ||
| - | {{Tabla75|celda2=[[Imagen:ptosmedios.png|300px]]|celda1= | ||
| '''Demostración:''' | '''Demostración:''' | ||
| - | + | Los triángulos ABC y MBN son semejantes por estar en la posición de Tales. Además la razón de semejanza es claramente 2, por lo que lo que se nos pide es bastante inmediato. | |
| - | + | ||
| - | }} | + | |
| }} | }} | ||
| Línea 88: | Línea 94: | ||
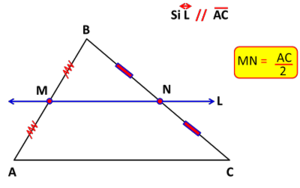
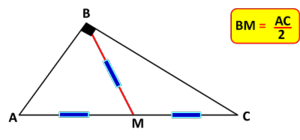
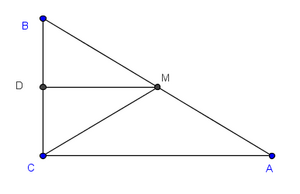
| Por M tracemos una paralela a CA, y sea D su punto de intersección con el cateto BC. Puesto que DM es paralela a CA y CA es perpendicular a BC, entonces DM es también perpendicular a BC. Por el teorema de los puntos medios se tiene que D es punto medio de BC ya que M lo es de AB). Pero entonces DM es mediatriz de BCM. De aquí que BM=CM (pues la mediatriz de un segmento es el lugar geométrico de los puntos que equidistan de los extremos). | Por M tracemos una paralela a CA, y sea D su punto de intersección con el cateto BC. Puesto que DM es paralela a CA y CA es perpendicular a BC, entonces DM es también perpendicular a BC. Por el teorema de los puntos medios se tiene que D es punto medio de BC ya que M lo es de AB). Pero entonces DM es mediatriz de BCM. De aquí que BM=CM (pues la mediatriz de un segmento es el lugar geométrico de los puntos que equidistan de los extremos). | ||
| + | }} | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas.
Aplicaciones de los criterios de semejanza Descripción: Ejercicios de aplicación de los criterios de semejanza de triángulos:
- Medición de alturas con sombras.
- Medición de alturas con espejos.
- ¿Cómo pudo medir Tales la altura de una pirámide?
Medición de alturas con espejos Descripción: En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica.
Medición de alturas con sombras Descripción: Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura..
Teorema de la bisectriz (8´43") Sinopsis: El teorema de la bisectriz dice:
"La bisectriz de un ángulo de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo"
 | 
|
Problema (aplicación del teorema de la bisectriz) (5´46") Sinopsis: Aplicación del teorema de la bisectriz.
Teorema de los puntos medios (7´47") Sinopsis:Problema:
En un triángulo ABC se traza la mediana CM y desde A se traza el segmento AN que corta a la mediana CM en su punto medio T. Sabiendo que TN = 5 cm, calcula el valor de AT.
Solución:
Véase el video para ver la solución.
| El problema anterior requiere la aplicación del teorema de los puntos medios:
Teorema de los puntos medios: "Si por el punto medio de uno de los lados de un triángulo se traza una recta paralela a un segundo lado, esta recta corta en su punto medio al tercer lado, la longitud del segmento que se determina es igual a la mitad de la longitud del lado al cual es paralela." | 
|
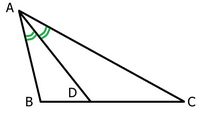
Demostración:
Los triángulos ABC y MBN son semejantes por estar en la posición de Tales. Además la razón de semejanza es claramente 2, por lo que lo que se nos pide es bastante inmediato.
Teorema de la mediana relativa a la hipotenusa (8´00") Sinopsis:| Problema:
Halla el valor de "x" en la figura:
Solución: Véase el video para ver la solución. |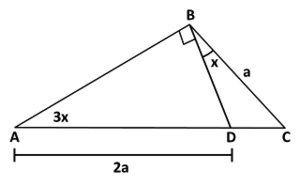 
|
| El problema anterior requiere la aplicación del teorema de la mediana relativa a la hipotenusa de un triángulo rectángulo:
Teorema de la mediana relativa a la hipotenusa: "La longitud de la mediana relativa a la hipotenusa de un triángulo rectángulo, es igual a la mitad de la longitud de la hipotenusa." | 
|
| Demostración:
Por M tracemos una paralela a CA, y sea D su punto de intersección con el cateto BC. Puesto que DM es paralela a CA y CA es perpendicular a BC, entonces DM es también perpendicular a BC. Por el teorema de los puntos medios se tiene que D es punto medio de BC ya que M lo es de AB). Pero entonces DM es mediatriz de BCM. De aquí que BM=CM (pues la mediatriz de un segmento es el lugar geométrico de los puntos que equidistan de los extremos). | 
|
