Plantilla:Teoremas del cateto y de la altura
De Wikipedia
| Revisión de 15:06 18 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:53 18 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 91: | Línea 91: | ||
| |sinopsis=Problema de aplicación del teorema de la altura | |sinopsis=Problema de aplicación del teorema de la altura | ||
| |url1=http://www.unicoos.com/video/matematicas/2-eso/semejanza-y-teorema-de-thales/teorema-de-tales/teorema-de-la-altura-y-thales | |url1=http://www.unicoos.com/video/matematicas/2-eso/semejanza-y-teorema-de-thales/teorema-de-tales/teorema-de-la-altura-y-thales | ||
| + | }} | ||
| + | {{Video_enlace_childtopia | ||
| + | |titulo1=Problema 3 | ||
| + | |duracion=5'34" | ||
| + | |sinopsis=Una torre eléctrica está sujeta al suelo con dos tensores. La distancia entre los pies de ambos tensores es 50 m, y los cables que sujetan la torre miden 30 y 40 m, respectivamente. Calcula la altura de la torre. | ||
| + | |url1=https://www.youtube.com/watch?v=ewOdTEsDF3U | ||
| }} | }} | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 16:53 18 sep 2017
Tutorial en el que se demuestra tanto el teorema de la altura como del cateto y aplica dichos teorema a la representación en la recta numérica de raíces cuadradas.
- 00:00 a 10:00: Demostración del Teorema de la Altura y del Cateto mediante la semejanza de triángulos.
- 10:00 a 10:35: Enunciado del Teorema de la Altura.
- 10:40 a 11:10: Enunciado del Teorema del Cateto.
- 11:10 a 15:40: Aplicación del Teorema de Pitágoras para representar raíces cuadradas..
- 15:50 a 19:45: Aplicación del Teorema de la Altura para representar raíces cuadradas..
- 19:45 a 22:15: Aplicación del Teorema del Cateto para representar raíces cuadradas.
Teorema del cateto En todo triángulo rectángulo, un cateto, 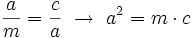 Y análogamente con el otro cateto, 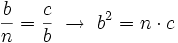 Demostración: Véase cualquiera de los siguientes videotutoriales.
Uno de los catetos de un triángulo rectángulo mide 16.5 cm y su proyección sobre la hipotenusa mide 7.5 cm. Halla el otro cateto, la proyección del otro cateto sobre la hipotenusa y la altura sobre la hipotenusa. En un triángulo rectángulo los catetos miden 20 y 21 cm. Calcula el valor de las proyecciones de los catetos sobre la hipotenusa. Teorema de la altura En todo triángulo rectángulo, la altura, 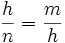 Demostración: Véase cualquiera de los siguientes videotutoriales:
Las proyecciones de los actetos sobre la hipotenusa de un triángulo rectángulo miden 18 m y 32 m, respectivamente. Halla la medida de los catetos y la de la altura sobre la hipotenusa. Problema de aplicación del teorema de la altura Una torre eléctrica está sujeta al suelo con dos tensores. La distancia entre los pies de ambos tensores es 50 m, y los cables que sujetan la torre miden 30 y 40 m, respectivamente. Calcula la altura de la torre. |
 , es media proporcional entre la hipotenusa,
, es media proporcional entre la hipotenusa, 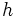 , y la proyección,
, y la proyección,  , de dicho cateto sobre la hipotenusa,
, de dicho cateto sobre la hipotenusa,  .
.
 , y su proyección,
, y su proyección,  .
.


