Plantilla:Poliedros: pirámide

De Wikipedia

(Diferencia entre revisiones)
Revisión de 10:34 26 sep 2017
Coordinador (Discusión | contribuciones)

← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)

Línea 1: Línea 1:
-{{Tabla75|celda1=+{{Definición de pirámide}}
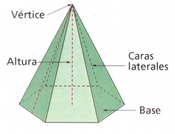
-{{Caja_Amarilla|texto=*Una '''pirámide''' es un poliedro, cuya '''base''' es un polígono cualquiera y cuyas '''caras laterales''' son triángulos con un vértice común, que se denomina '''vértice''' de la pirámide.+
-*La '''altura''' de la pirámide es la distancia del el vértice al plano de la base.+
-}}+
{{p}} {{p}}
-{{Video_enlace_estudiia+===Clasificación de las pirámides===
-|titulo1=Pirámide+{{Clasificación de las pirámides}}
-|duracion=3'52"+
-|sinopsis=Pirámide: definición y elementos.+
-|url1=https://www.youtube.com/watch?v=ZyftAKtrAHc&index=19&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm+
-}}+
{{p}} {{p}}
-====Clasificación de las pirámides====+===Desarrollo plano de una pirámide===
-{{Caja_Amarilla|texto=+{{Desarrollo plano pirámide}}
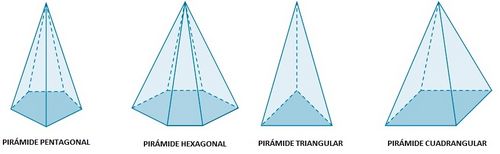
-*'''Atendiendo a sus bases:''' En función del polígono base, las pirámides pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.{{p}}+
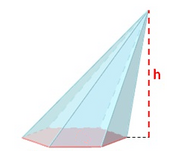
-*'''Atendiendo a su inclinación:''' Si la proyección ortogonal del vértice sobre la base coincide con su centro, la pirámide es '''recta''', si no , es '''oblicua'''.+
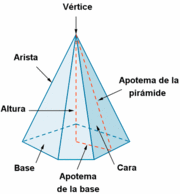
-*'''Atendiendo a su regularidad:''' Una pirámide es '''regular''' si su base es un polígono regular. En caso contrario es '''irregular'''. En una pirámide regular, todas las aristas laterales son iguales y las caras laterales son triángulos isósceles iguales. La altura de cada uno de ellos se llama '''apotema de la pirámide'''.}}+
-|celda2=[[Imagen:piramiderecta.png|center|175px]]<center>Piramide recta</center><br>[[Imagen:piramideoblicua.png|center|175px]]<center>Pirámide oblicua</center>+
-}}+
-{{Tabla75|celda2=[[Imagen:elementos_piramide.gif|center|180px]]<br>Elementos de una pirámide regular<br><center><sup>''de http://calculo.cc''</sup></center>+
-|celda1=+
-{{Video_enlace_estudiia+
-|titulo1=Clasificación de las pirámides+
-|duracion=3'34"+
-|sinopsis=Clasificación de las pirámides.+
-|url1=https://www.youtube.com/watch?v=-jw4nPA-2Rw&index=20&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm+
-}}+
-{{p}}+
-[[Imagen:clasif_piramide.jpg|center|500px]]<br><center>Clasificación de las pirámides atendiendo a su base<br><sup>''de http://calculo.cc''</sup></center>+
-{{p}}+
-{{Geogebra_enlace+
-|descripcion=En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados.+
-|enlace=[https://ggbm.at/XrcfnFaT Elementos de una pirámide]+
-}}+
-{{p}}+
-{{Video_enlace_abel+
-|titulo1=Pirámides y pirámides regulares+
-|duracion=5'10"+
-|sinopsis=Definiciones, elementos y propiedades.+
-|url1=https://www.youtube.com/watch?v=8WubFM4e9ZI+
-}}+
- +
-}}+
-====Desarrollo plano de una pirámide====+
-{{Caja_Amarilla|texto=Si representamos en un plano todas las caras de una pirámide, de forma contigua, obtenemos lo que se denomina '''desarrollo plano''' de la pirámide.}}+
-{{p}}+
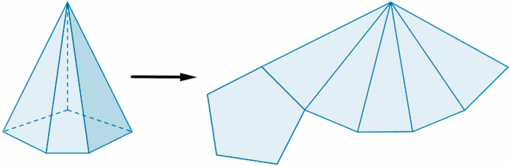
-Fíjate en la siguiente pirámide pentagonal. Si la cortásemos adecuadamente siguiendo ciertas aristas, podríamos desplegarla como se muestra en la siguiente figura.+
-{{p}}+
-[[Imagen:deasarrollo_piramide.gif|center|550px]]<br><center>Desarrollo plano de una pirámide <br><sup>''de http://calculo.cc''</sup></center>+
{{p}} {{p}}

Revisión actual

  • Una pirámide es un poliedro, cuya base es un polígono cualquiera y cuyas caras laterales son triángulos con un vértice común, que se denomina vértice de la pirámide.
  • La altura de la pirámide es la distancia del el vértice al plano de la base.
  • Las aristas básicas son los lados del polígono base.
  • Las aristas laterales son las aristas que unen el vértice con la base.

Pirámide     Descripción:

Actividad en la que se presenta la pirámide y sus elementos.

Pirámide (3'52")     Sinopsis:

Pirámide: definición y elementos.

Piramide recta

[editar]

Clasificación de las pirámides

  • Atendiendo a sus bases: En función del polígono base, las pirámides pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.

  • Atendiendo a su inclinación: Si la proyección ortogonal del vértice sobre la base coincide con su centro, la pirámide es recta, si no , es oblicua.
  • Atendiendo a su regularidad: Una pirámide es regular si su base es un polígono regular. En caso contrario es irregular. En una pirámide regular, todas las aristas laterales son iguales y las caras laterales son triángulos isósceles iguales. La altura de cada uno de ellos se llama apotema de la pirámide.
Pirámide oblicua
de http://universoformulas.com
Clasificación de las pirámides (3'34")     Sinopsis:

Clasificación de las pirámides.

Pirámides regulares     Descripción:

Actividad en la que se presentan distintos tipos de pirámides regulares.


Clasificación de las pirámides atendiendo a su base
de http://calculo.cc

Elementos de una pirámide regular     Descripción:

En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados.

Pirámides y pirámides regulares (5'10")     Sinopsis:

Definiciones, elementos y propiedades.


Elementos de una pirámide regular
de http://calculo.cc
Ejercicio (3'49")     Sinopsis:

Dibuja un pirámide de base cuadrangular regular y una pirámide de base triangular irregulr. Recuenta sus caras, vértices y aristas.

Autoevaluación: Pirámides     Descripción:

Ejecicios de autoevaluación sobre la pirámide.

[editar]

Desarrollo plano de una pirámide

Si representamos en un plano todas las caras de una pirámide, de forma contigua, obtenemos lo que se denomina desarrollo plano de la pirámide.

Fíjate en la siguiente pirámide pentagonal. Si la cortásemos adecuadamente, siguiendo ciertas aristas, podríamos desplegarla como se muestra en la siguiente figura.


Desarrollo plano de una pirámide pentagonal regular
de http://calculo.cc

Desarrollo de una pirámide recta regular     Descripción:

Actividad en la que podrás ver el desarrollo plano de distintas pirámides rectas regulares.

Ejercicio (1'08")     Sinopsis:

Dibuja el desarrollo plano del siguiente poliedro.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Poliedros:_pir%C3%A1mide"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda