Troncos de conos (2º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:52 1 oct 2017 Coordinador (Discusión | contribuciones) (→Tronco de pirámide) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Superficie del tronco de cono) |
||
| Línea 13: | Línea 13: | ||
| *Un tronco de cono tiene dos '''bases''' , la del cono original y la sección producida al cortar con el plano. Ambas son círculos. | *Un tronco de cono tiene dos '''bases''' , la del cono original y la sección producida al cortar con el plano. Ambas son círculos. | ||
| *La '''altura''' del tronco de cono es la distancia entre sus dos bases. | *La '''altura''' del tronco de cono es la distancia entre sus dos bases. | ||
| + | *La '''generatriz''' del tronco de cono es la porción de generatriz del cono de partida que queda tras el truncamiento. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 18: | Línea 19: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | En la figura de la derecha están representados los distintos elementos de un tronco de pirámide regular: | + | {{Tabla75|celda1= |
| - | *'''B, b:''' Bases mayor y menor. | + | En la figura de la derecha están representados los distintos elementos de un tronco de cono: |
| + | {{p}} | ||
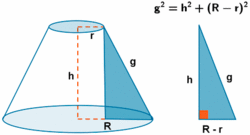
| *'''h:''' altura. | *'''h:''' altura. | ||
| - | *'''Ap:''' apotema del tronco. | + | *'''g:''' generatriz del tronco. |
| - | *'''ap, ap':''' apotemas de las bases mayor y menor. | + | *'''r, R:''' radios delas bases menor y mayor. |
| - | |celda2=[[Imagen:tronco_piramide_apotema.gif|center|250px]]<center>Elementos de un tronco de pirámide<br><sup>''de http://calculo.cc''</sup></center> | + | {{p}} |
| - | + | Fíjate como están relacionados entres sí estos elementos mediante el teorema de Pitágoras. Además del teorema de Pitágoras, también podemos hacer uso de la semejanza de triángulos para relacionar los elementos del tronco de cono con los del cono de partida, como puedes ver en el siguiente ejercicio. | |
| + | {{p}} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=3'08" | ||
| + | |sinopsis=Un cono tiene 10 cm de radio de la base y 20 cm de altura. Lo truncamos mediante un plano paralelo a la base, de manera que se desprende un cono de 6 cm de altura. Halla el radio menor del cono truncado utilizando triángulos semejantes. | ||
| + | |url1=https://www.youtube.com/watch?v=As-y-mKJXxE | ||
| + | }} | ||
| + | |celda2=[[Imagen:tronco_cono_2.gif|center|250px]]<center>Elementos de un tronco de cono<br><sup>''de http://calculo.cc''</sup></center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 33: | Línea 43: | ||
| Fíjate en el siguiente tronco de cono. Si la cortásemos adecuadamente, podríamos desplegarlo como se muestra en la siguiente figura. | Fíjate en el siguiente tronco de cono. Si la cortásemos adecuadamente, podríamos desplegarlo como se muestra en la siguiente figura. | ||
| {{p}} | {{p}} | ||
| - | [[Imagen:deasarrollo_tronco_cono.jpg|center|500px]]<br><center>Desarrollo plano de un tronco de cono<br><sup>''de http://universoformulas.com''</sup></center> | + | [[Imagen:deasarrollo_tronco_cono.jpg|center|300px]]<br><center>Desarrollo plano de un tronco de cono<br><sup>''de http://universoformulas.com''</sup></center> |
| {{p}} | {{p}} | ||
| + | |||
| ==Superficie del tronco de cono== | ==Superficie del tronco de cono== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Línea 42: | Línea 53: | ||
| {{p}}{{Tabla3 | {{p}}{{Tabla3 | ||
| |celda1= | |celda1= | ||
| - | <center>[[Imagen:conotruncado.png]]</center> | + | <center>[[Imagen:conotruncado.png|200px]]</center> |
| |celda2={{p}} | |celda2={{p}} | ||
| * '''Área:'''{{p}} | * '''Área:'''{{p}} | ||
| Línea 57: | Línea 68: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Ejercicios: ''Área del tronco de cono''|enunciado= | + | {{Geogebra_enlace |
| - | {{Video_enlace | + | |descripcion=En esta escena podrás calcular el volumen y las áreas de un tronco de cono. |
| - | |titulo1=Ejercicio 1 | + | |enlace=[https://ggbm.at/pRFB6c5R Áreas del tronco de cono] |
| - | |duracion= | + | }} |
| - | |sinopsis= | + | |
| - | |url1= | + | |
| - | }}}} | + | |
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
Revisión actual
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 228)
[editar]
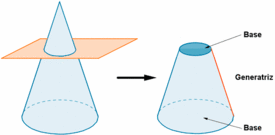
Tronco de cono
|  Tronco de cono
de http://calculo.cc |
En la figura de la derecha están representados los distintos elementos de un tronco de cono:
Fíjate como están relacionados entres sí estos elementos mediante el teorema de Pitágoras. Además del teorema de Pitágoras, también podemos hacer uso de la semejanza de triángulos para relacionar los elementos del tronco de cono con los del cono de partida, como puedes ver en el siguiente ejercicio.  Ejercicio (3'08") Sinopsis:Un cono tiene 10 cm de radio de la base y 20 cm de altura. Lo truncamos mediante un plano paralelo a la base, de manera que se desprende un cono de 6 cm de altura. Halla el radio menor del cono truncado utilizando triángulos semejantes. |  Elementos de un tronco de cono
de http://calculo.cc |
[editar]
Desarrollo plano del tronco de cono
Si representamos en un plano todas las caras de un tronco de cono, de forma contigua, obtenemos lo que se denomina desarrollo plano del tronco de cono.
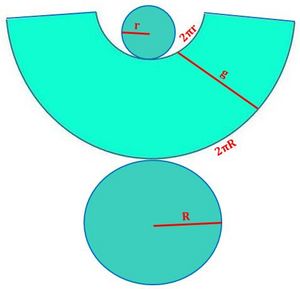
Fíjate en el siguiente tronco de cono. Si la cortásemos adecuadamente, podríamos desplegarlo como se muestra en la siguiente figura.
Desarrollo plano de un tronco de cono
de http://universoformulas.com
de http://universoformulas.com
[editar]
Superficie del tronco de cono
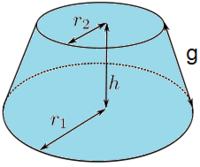
La superficie o área del tronco de cono es igual a la suma del área de las dos bases y del área lateral.
- El área de las bases es la suma de las áreas de dos círculos.
- El área lateral es igual a la diferencia de las áreas laterales de dos conos, el de partida y el que se desprende al truncarlo.
 |
|
|
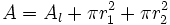
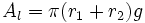
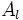: Área lateral.
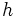: altura.
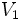: Volumen del cono completo.
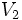: Volumen del cono pequeño eliminado.
Áreas del tronco de cono Descripción: En esta escena podrás calcular el volumen y las áreas de un tronco de cono.
[editar]
Ejercicios propuestos
 Ejercicios propuestos: Tronco de cono (Pág. 228)
|
