Esferas (2º ESO)
De Wikipedia
| Revisión de 17:21 1 oct 2017 Coordinador (Discusión | contribuciones) (→Superficie de la esfera) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Superficie de la esfera) |
||
| Línea 11: | Línea 11: | ||
| {{Definición de esfera}} | {{Definición de esfera}} | ||
| {{p}} | {{p}} | ||
| - | ==Superficie de la esfera== | + | ===Superficie de la esfera=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| {{Tabla3 | {{Tabla3 | ||
| Línea 25: | Línea 25: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás calcular el volumen y área de un balón de futbol. | ||
| + | |enlace=[https://ggbm.at/DRMa7bXj Área de la esfera] | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales|titulo=Área de la esfera|enunciado= | ||
| + | {{Video_enlace_abel | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=15'22" | ||
| + | |sinopsis=La esfera: | ||
| + | *Definición. | ||
| + | *Elementos | ||
| + | *Área y volumen. | ||
| + | *Ejercicio. | ||
| + | |url1=https://www.youtube.com/watch?v=XZtPQf9elFk | ||
| + | }} | ||
| + | {{Video_enlace_tutomate | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=4'09" | ||
| + | |sinopsis=Cálculo del área total y el volumen ocupado por una esfera de radio r. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=dvJiJrZf_U8 | ||
| + | }} | ||
| + | ---- | ||
| {{Video_enlace_math2me | {{Video_enlace_math2me | ||
| - | |titulo1=Ejercicios | + | |titulo1=Problemas 1 |
| |duracion=3'40" | |duracion=3'40" | ||
| |sinopsis=#Halla el área de una esfera de radio 1 m. | |sinopsis=#Halla el área de una esfera de radio 1 m. | ||
| #Halla el área de una esfera inscrita en un cubo de 10 cm de arista. | #Halla el área de una esfera inscrita en un cubo de 10 cm de arista. | ||
| |url1=https://www.youtube.com/watch?v=57b7j0j0aNo | |url1=https://www.youtube.com/watch?v=57b7j0j0aNo | ||
| + | }} | ||
| + | {{Video_enlace_estudiia | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=2'36" | ||
| + | |sinopsis=Halla el volumen y el área de una esfera de diámetro 10 cm. | ||
| + | |url1=https://www.youtube.com/watch?v=sr6YgplUkcM&index=32&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Propiedad|enunciado=La superficie de una esfera coincide con la superficie lateral del cilindro que la envuelve, es decir, del cilindro en la cual se halla inscrita.}} | + | {{Teorema|titulo=Propiedad|enunciado=La superficie de una esfera coincide con la superficie lateral del cilindro en la cual se halla inscrita. |
| + | |demo= | ||
| + | {{Tabla75|celda2=[[Imagen:esfera_cilindro.jpg|170px]] | ||
| + | |celda1=Consideremos una esfera de radio r. Si la esfera se halla inscrita en un cilindro, éste tendrá radio r y altura o generatriz 2r. En consecuencia, el área lateral de dicho cilindro será: | ||
| + | |||
| + | <center><math>A_l = 2 \pi r g = 2 \pi r 2r = 4 \pi r^2\;</math></center> | ||
| + | |||
| + | por lo que coincide con el área de la esfera. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | ==Casquete y zona esférica== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | *Un '''casquete esférico''' es la parte de una esfera cortada por un plano. | ||
| + | *Una '''zona esférica''' o '''segmento esférico''' es la parte de una esfera limitada por dos planos que la seccionan. | ||
| + | }} | ||
| + | {{p}} | ||
| + | [[Imagen:casquete_y_zona_esfericos_1.jpg|550px|center]] | ||
| + | {{p}} | ||
| + | ===Superficie del casquete y de la zona esférica=== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | {{Tabla3 | ||
| + | |celda1= | ||
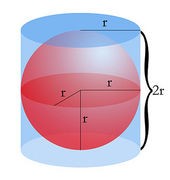
| + | <center>[[Imagen:casquete_y_zona_esfericos.jpg|500px]]<br>Casquete y zona esférica<br><sup>de ''http://calculo.cc''</sup></center> | ||
| + | |celda2={{p}} | ||
| + | * '''Área:'''{{p}} | ||
| + | {{Caja|contenido=<math>A=2 \pi Rh \;\!</math>}}{{p}} | ||
| + | |celda3={{p}} | ||
| + | * '''Elementos:'''{{p}} | ||
| + | :<math>R\;\!</math>: radio de la esfera. | ||
| + | :<math>h\;\!</math>: altura del casquete o zona esférica. | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema|titulo=Propiedad|enunciado=La superficie de un casquete o de la zona esférica coincide con la porción de superficie lateral, de la misma altura, del cilindro en el cual se halla inscrita la esfera. | ||
| + | |demo= | ||
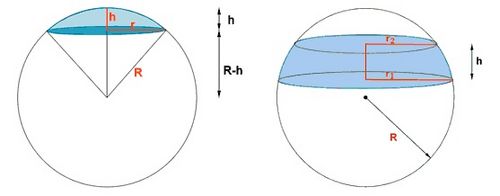
| + | {{Tabla75|celda2=[[Imagen:zona_cilindro_area.jpg|500px|center]]<br><center>Zona esférica y porción de cilindro con la misma altura, h<br><sup>de ''http://aulafacil.com''</sup></center>|celda1=Consideremos una esfera de radio R y sea h la altura del casquete o de la zona esférica. El cilindro en el que está inscrita la esfera también tendrá radio R, y si consideramos la porción de cilindro de altura o generatriz h, el área lateral de dicha porción de cilindro será: | ||
| + | <br> | ||
| + | <center><math>A_l = 2 \pi r g = 2 \pi R h \;</math></center> | ||
| + | <br> | ||
| + | por lo que coincide con el área del casquete o de la zona esférica. | ||
| + | }} | ||
| + | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 230)
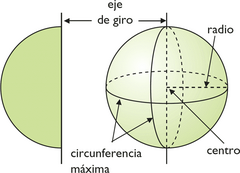
Esfera
Una esfera es un cuerpo de revolución que se obtiene haciendo girar un semicírculo alrededor de su diámetro. Elementos de la esfera:
|
Actividades en la que podrás ver cómo se genera una esfera y estudiar sus elementos.
Superficie de la esfera
En esta escena podrás calcular el volumen y área de un balón de futbol.
La esfera:
- Definición.
- Elementos
- Área y volumen.
- Ejercicio.
Cálculo del área total y el volumen ocupado por una esfera de radio r. Ejemplos.
- Halla el área de una esfera de radio 1 m.
- Halla el área de una esfera inscrita en un cubo de 10 cm de arista.
Halla el volumen y el área de una esfera de diámetro 10 cm.
Propiedad
La superficie de una esfera coincide con la superficie lateral del cilindro en la cual se halla inscrita.
Casquete y zona esférica
- Un casquete esférico es la parte de una esfera cortada por un plano.
- Una zona esférica o segmento esférico es la parte de una esfera limitada por dos planos que la seccionan.
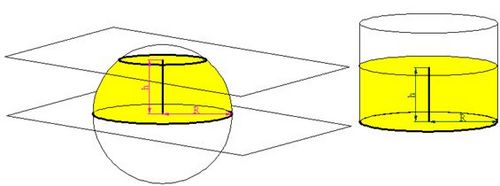
Superficie del casquete y de la zona esférica
|
|
Propiedad
La superficie de un casquete o de la zona esférica coincide con la porción de superficie lateral, de la misma altura, del cilindro en el cual se halla inscrita la esfera.
| Consideremos una esfera de radio R y sea h la altura del casquete o de la zona esférica. El cilindro en el que está inscrita la esfera también tendrá radio R, y si consideramos la porción de cilindro de altura o generatriz h, el área lateral de dicha porción de cilindro será:
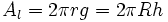
| Zona esférica y porción de cilindro con la misma altura, h
de http://aulafacil.com |
Ejercicios propuestos
|
Ejercicios propuestos: Esferas |
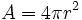
 : radio.
: radio.
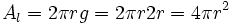

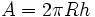
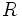 : radio de la esfera.
: radio de la esfera.
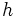 : altura del casquete o zona esférica.
: altura del casquete o zona esférica.