El significado de las fracciones (1º ESO)
De Wikipedia
| Revisión de 18:58 12 oct 2017 Coordinador (Discusión | contribuciones) (→Las fracciones) ← Ir a diferencia anterior |
Revisión de 18:59 12 oct 2017 Coordinador (Discusión | contribuciones) (→Ejercicios y problemas) Ir a siguiente diferencia → |
||
| Línea 163: | Línea 163: | ||
| }} | }} | ||
| {{AI_anaya | {{AI_anaya | ||
| - | |titulo1=Autoevaluación: ''La fracción como operador'' | + | |titulo1=Problemas: ''La fracción como operador'' |
| |descripcion= | |descripcion= | ||
Revisión de 18:59 12 oct 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 122)
Introducción
Un toque divertido para empezar el tema:
Si no fuera por las fracciones ni Troncho ni Poncho ni nadie podría celebrar su cumpleaños.
Puedes encontrar ejercicios sobre este vídeo y material similar en: http://www.angelitoons.com/
Actividades en las que se resume lo que se va a ver en este tema.
Las fracciones
Cuando necesitamos expresar cantidades con partes de la unidad, además de los números decimales, disponemos de las fracciones.
- Una fracción es un número que expresa una cantidad determinada de porciones que se toman de un todo dividido en partes iguales. Se representa
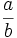 , o bien,
, o bien, 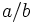 :
:
- A
 se le llama denominador y representa las partes en que se divide la unidad.
se le llama denominador y representa las partes en que se divide la unidad.
- A
- A
 se le llama numerador y representa las porciones que tomamos.
se le llama numerador y representa las porciones que tomamos.
- A
- El valor de la fracción es el número que resulta de dividir el numerador entre el denominador.
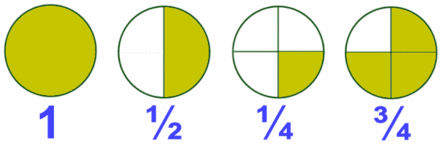
En la Fig. 1 tienes algunos ejemlos de fracciones representadas mendiante los llamados diagramas de tarta.
El valor de cada fracción se obtiene dividiendo el numerador entre el denominador:
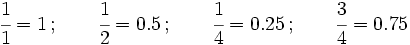
Fíjate que la unidad se puede representar mediante una fracción que tenga el mismo numerador que denominador.
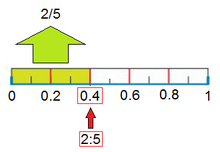
En la Fig. 2 está representada la fracción 2/5. Fíjate como al hacer la división 2:5=0.4, se obtienen 4 décimas, que ocupan la misma porción que la fracción 2/5. Es decir, una fracción equivale a una división indicada.
Concepto de fracción. Fracciones propias e impropias.
Ejercicios de autoevaluación sobre el significado de las fracciones.
Representación gráfica de fracciones y de su expresión decimal.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
- Actividad en la que se muestra y practica el concepto de fracción.
- Actividad en la que se explica y practica la representación de fracciones en la recta numérica.
Actividades en las que se explica y practica cómo se lee una fracción.
Fracciones propias e impropias
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Proposición Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como número mixto. La fracción
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa. Conversión de fracción impropia a número mixto Conversión de fracción impropia a número mixto. Conversión de fracción impropia a número mixto. Escribiendo una fracción impropia com un número mixto Convierte a número mixto la siguiente fracción impropia: Nota: En el video, la división está realizada por el método anglosajón Convierte a número mixto la siguiente fracción impropia: Nota: En el video, la división está realizada por el método anglosajón Conversión de número mixto a fracción impropia Conversión de número mixto a fracción impropia. Conversión de número mixto a fracción impropia. Convierte a fracción impropia el siguiente número mixto: Nota: En el video, la división está realizada por el método anglosajón Convierte a fracción impropia el siguiente número mixto: Nota: En el video, la división está realizada por el método anglosajón Números mixtos y fracciones impropias. Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
La fracción como operador
Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos.
Fracción de una cantidad
Para calcular una fracción a/b de una cantidad C se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por C).
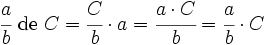
Ejemplo 1: Cálculo de la parte conocido el total
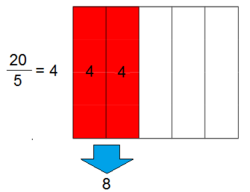
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada.
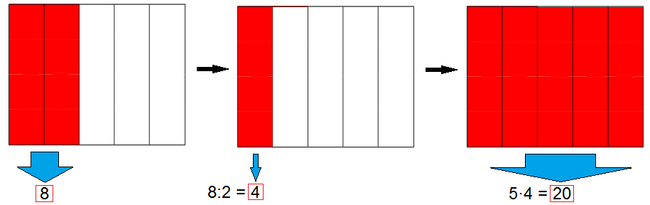
Ejemplo 2: Cálculo del total conocida la parte
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?
La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
Ejercicios y problemas
Problemas sencillos con fracciones resueltos.
Ejercicios de autoevaluación sobre fracciones.
|
Ejercicios propuestos: El significado de las fracciones |
|
Ejercicios propuestos: Problemas con fracciones |
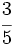 es una fracción propia porque 3 < 5.
es una fracción propia porque 3 < 5.
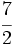 es una fracción impropia porque 7 > 2.
es una fracción impropia porque 7 > 2.
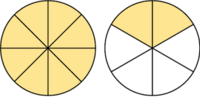
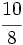 es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
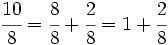
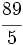
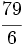

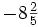
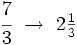 ; B)
; B) 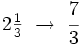
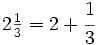
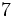

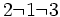 ; B)
; B) 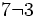
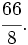
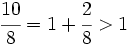
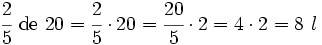
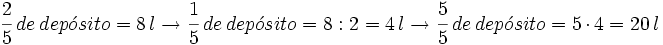
 = capacidad del depósito.
= capacidad del depósito.