Plantilla:Poliedros regulares
De Wikipedia
| Revisión de 11:17 30 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 15:56 14 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| </table> | </table> | ||
| {{p}} | {{p}} | ||
| - | {{Tabla50|celda1= | ||
| {{AI_cidead | {{AI_cidead | ||
| |titulo1=Poliedros regulares | |titulo1=Poliedros regulares | ||
| Línea 110: | Línea 109: | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena8/2quincena8_contenidos_2i.htm | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena8/2quincena8_contenidos_2i.htm | ||
| }} | }} | ||
| - | |celda2= | ||
| [[Imagen:desarrollo_poli_reg.jpg|center]]<br><center>Desarrollo plano de los poliedros regulares</center> | [[Imagen:desarrollo_poli_reg.jpg|center]]<br><center>Desarrollo plano de los poliedros regulares</center> | ||
| - | }} | ||
| {{p}} | {{p}} | ||
Revisión de 15:56 14 oct 2017
- Poliedro regular es aquel que cumple:
- Sus caras son polígonos regulares iguales.
- Todos los vértices tienen el mismo orden.
- Sólo hay cinco poliedros regulares, los llamados sólidos platónicos: tetraedro, cubo, octaedro, dodecaedro e icosaedro.
 |
 |
 |
 |
 |
Poliedros regulares Descripción: Actividad en la que se presentan los 5 poliedros regulares y se hace un recuento de sus elementos.
Poliedros regulares (2'52") Sinopsis:Videotutorial.
El tetraedro regular (23'36") Sinopsis:El tetraedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El hexaedro regular o cubo (20'05") Sinopsis:El hexaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
El octaedro regular (28'00") Sinopsis:El octaedro regular:
- Definición.
- Desarrollo plano.
- Área y volumen.
- Ejercicio.
Ejercicio (5'03") Sinopsis:Calcula el área de un dodecaedro de 6 cm de arista y 4 cm de radio.
Poliedros regulares Descripción: En esta escena podrás ver y rotar los poliedros regulares.
Tetraedro Descripción: Actividades sobre el tetraedro.
Octaedro Descripción: Actividades sobre el octaaedro.
Hexaedro o cubo Descripción: Actividades sobre el hexaedro o cubo.
Dodecaedro Descripción: Actividades sobre el dodecaedro.
Autoevaluación: Poliedros regulares Descripción: Ejecicios de autoevaluación sobre poliedros regulares.
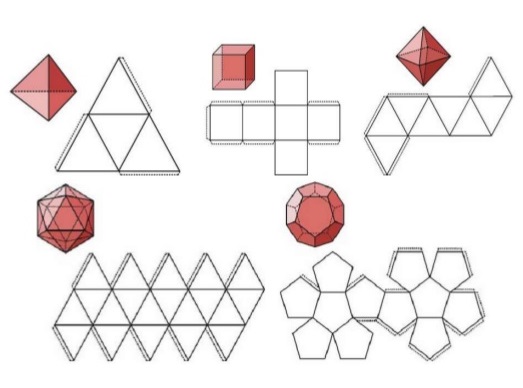
Desarrollo plano de los poliedros regulares
Si representamos en un plano todas las caras de un poliedro, de forma contigua, obtenemos lo que se denomina desarrollo plano del poliedro.
Si cortásemos adecuadamente cada uno de los poliedros regulares, siguiendo ciertas aristas, podríamos desplegarlos como se muestra en la imagen adjunta.
Desarrollo plano de los poliedros regulares Descripción: Actividad en la que se muestra el desarrollo plano de los 5 poliedros regulares.
