Plantilla:Clasificación de las pirámides
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 06:09 28 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 33: | Línea 33: | ||
| |url1=https://www.youtube.com/watch?v=8WubFM4e9ZI | |url1=https://www.youtube.com/watch?v=8WubFM4e9ZI | ||
| }} | }} | ||
| - | |||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_childtopia |
| + | |titulo1=Ejercicio | ||
| + | |duracion=3'49" | ||
| + | |sinopsis=Dibuja un pirámide de base cuadrangular regular y una pirámide de base triangular irregulr. Recuenta sus caras, vértices y aristas. | ||
| + | |url1=https://www.youtube.com/watch?v=kCNgIOtLwjI | ||
| + | }} | ||
| {{AI_vitutor | {{AI_vitutor | ||
| |descripcion=Ejecicios de autoevaluación sobre la pirámide. | |descripcion=Ejecicios de autoevaluación sobre la pirámide. | ||
| - | |url1=https://www.vitutor.com/geo/esp/f_4e.html | + | |url1=http://www.vitutor.com/geo/esp/f_4e.html |
| |titulo1=Autoevaluación: ''Pirámides'' | |titulo1=Autoevaluación: ''Pirámides'' | ||
| }} | }} | ||
Revisión actual
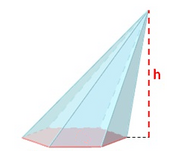
| Pirámide oblicua
de http://universoformulas.com |
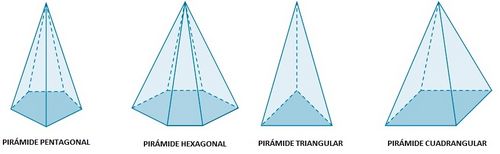
Clasificación de las pirámides. Actividad en la que se presentan distintos tipos de pirámides regulares. Clasificación de las pirámides atendiendo a su base
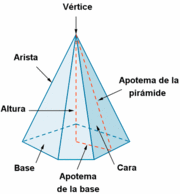
de http://calculo.cc En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. Definiciones, elementos y propiedades. | Elementos de una pirámide regular
de http://calculo.cc |
Dibuja un pirámide de base cuadrangular regular y una pirámide de base triangular irregulr. Recuenta sus caras, vértices y aristas.
Ejecicios de autoevaluación sobre la pirámide.