Plantilla:Sistemas de ecuaciones lineales 2x2

(Diferencia entre revisiones)

Revisión de 11:51 16 oct 2017

Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2 de ecuaciones lineales, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:

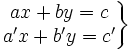
$\left . \begin{matrix} ax+by=c \\ a'x+b'y=c'\end{matrix} \right \}$

Se llama solución de un sistema 2x2, a cualquier pareja de valores 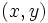$(x,y)\;$ que sea solución de ambas ecuaciones a la vez. Las soluciones de este tipo de sistemas son los puntos de corte de las rectas que representan cada una de las ecuaciones del sistema.

Ejemplo: Solución de un sistema de ecuaciones

Comprueba si las parejas de números (1,2) y (-1,3) son o no soluciones del sistema:

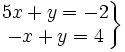
$\left . \begin{matrix} 5x+y=-2 \\ -x+y=4 \end{matrix} \right \}$

Solución:

Para comprobar si (1,2) es solución, sustituimos x=1 e y=2 en las dos ecuaciones del sistema:

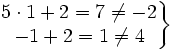
$\left . \begin{matrix} 5 \cdot 1+ 2=7 \ne -2 \\ -1+2=1 \ne 4 \end{matrix} \right \}$

Como no se verifican las dos ecuaciones, la pareja (1,2) no es solución del sistema.

Para comprobar si (-1,3) es solución, sustituimos x=-1 e y=3 en las dos ecuaciones del sistema:

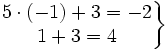
$\left . \begin{matrix} 5 \cdot (-1)+ 3=-2 \\ 1+3= 4 \end{matrix} \right \}$

Ahora si se verifican las dos ecuaciones, por tanto, la pareja (-1,3) si es solución del sistema.

Sistema de ecuaciones lineales (1´00") Sinopsis:

Autoevaluación: Sistemas de ecuaciones lineales Descripción:

Ejercicios de autoevaluación sobre sistemas de ecuaciones lineales.

 }}
 {{p}}
+{{Video_enlace_angelmartinez
+|titulo1=Sistema de ecuaciones lineales
+|duracion=1´00"
+|url1=https://www.youtube.com/watch?v=i7DMkFyfNpU
+|sinopsis=*Ecuación lineal con dos incógnitas. Soluciones.
+*Sistema de ecuaciones lineales con dos incógnitas. Soluciones.
+}}
 {{AI_vitutor
 |titulo1=Autoevaluación: ''Sistemas de ecuaciones lineales''