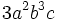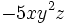Plantilla:Monomios
De Wikipedia
| Revisión de 06:26 17 oct 2017 Coordinador (Discusión | contribuciones) (→Monomios semejantes) ← Ir a diferencia anterior |
Revisión de 06:34 17 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| }} | }} | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| - | |titulo1=Tutorial 2: | + | |titulo1=Tutorial 2 |
| |duracion=6'59" | |duracion=6'59" | ||
| |sinopsis=Monomios: Expresión general, coeficiente, parte literal y grado. | |sinopsis=Monomios: Expresión general, coeficiente, parte literal y grado. | ||
| - | |url1=https://www.youtube.com/watch?v=RYM3tdiS_LU | + | |url1=https://www.youtube.com/watch?v=RYM3tdiS_LU&index=1&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU |
| }} | }} | ||
| {{Video_enlace_paps | {{Video_enlace_paps | ||
| Línea 51: | Línea 51: | ||
| ---- | ---- | ||
| {{Video_enlace_childtopia | {{Video_enlace_childtopia | ||
| - | |titulo1=Ejercicio | + | |titulo1=Ejercicio 1 |
| |duracion=3'10" | |duracion=3'10" | ||
| |sinopsis=Indica el coeficiente, la parte literal y el grado de los siguientes monomios: <math>-3ab,~ 2x^2y^3,~ 5x,~ -6x^4\;</math> | |sinopsis=Indica el coeficiente, la parte literal y el grado de los siguientes monomios: <math>-3ab,~ 2x^2y^3,~ 5x,~ -6x^4\;</math> | ||
| |url1=https://www.youtube.com/watch?v=xdeqO2QHnw4 | |url1=https://www.youtube.com/watch?v=xdeqO2QHnw4 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=14'34" | ||
| + | |sinopsis=Ejercicios 1- 9: Identificar los monomios y sus partes. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=5UDW4J9EBVI&list=PLw7Z_p6_h3ow70kSFPZjp_toVtyxYkAaU&index=5 | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 06:34 17 oct 2017
- Monomio es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas a potencias de exponente natural.
- Se llama coeficiente de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si el coeficiente es un 1 no suele escribirse. Si el coeficiente es 0, el monomio resultante es el número 0.
- Se denomina grado de un monomio a la suma de los exponentes de las letras. Si no hay letras el grado es cero.
- a)
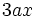es un monomio de grado 2 y coeficiente 3.
- b)
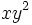es un monomio de grado 3 y coeficiente 1.
- c)
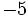es un monomio de grado 0 y coeficiente -5.
- d) En la siguiente escena se puede observar el coeficiente y el grado de un monomio. En la parte superior se pueden cambiar los exponentes de las letras a, b, y x. Para cambiar el coeficiente del monomio modifica la casilla de abajo.
Tutorial 1 (3'48") Sinopsis:- Álgebra.
- Valor numérico de una expresión algebraica.
- Tipos de expresiones algebraicas.
- Monomios.
- Partes y grado de un monomio.
Tutorial 2 (6'59") Sinopsis: Monomios: Expresión general, coeficiente, parte literal y grado.
Tutorial 3: Grado de un monomio (3'48") Sinopsis: Aprende a calcular el grado relativo y absoluto de un monomio.
Nota: Al "grado absoluto" de un monomio se le llama simplemente "grado" del monomio.
Ejercicio 1 (3'10") Sinopsis:Indica el coeficiente, la parte literal y el grado de los siguientes monomios: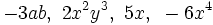 
Ejercicio 2 (14'34") Sinopsis: Ejercicios 1- 9: Identificar los monomios y sus partes.
Grado y elementos de un monomio Descripción: Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio.
Autoevaluación: Grado y elementos de un monomio Descripción: Ejercicios de autoevaluación sobre el grado y los elementos de un monomio.
Actividad: Grado de un monomio Indica el grado y el coeficiente de los siguientes monomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Monomios semejantes
Son monomios semejantes aquellos en los que aparecen las mismas letras con los mismos exponentes.
Son monomios semejantes: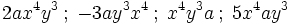 
Las letras pueden aparecer en distinto orden ya que por la propiedad conmutativa las podemos reordenar.
Monomios: elementos, grado, semejanza y opuestos. Descripción: Actividades en la que aprenderás y practicarás a hallar los elementos y el grado de un monomio. También practicaras con monomios semejantes y opuestos.
Tutorial 1 (2'00") Sinopsis: Aprende a distiguir cuando dos monomios son o no semejantes.
Tutorial 2 (4'45") Sinopsis: Aprende a distiguir cuando dos monomios son o no semejantes.
Tutorial 3 (5'11") Sinopsis: Aprende a distiguir cuando dos monomios son o no semejantes.
Tutorial 4 (2'40") Sinopsis:Monomios semejantes. Ejemplos.
Tutorial 5 (2'40") Sinopsis: Valor numérico de un monomio. Monomios constantes, monomios nulos y monomios semejantes. Ejemplos.
Ejercicio (1'38") Sinopsis: Encuentra los términos semejantes.
