Plantilla:Cálculo de los divisores de un número
De Wikipedia
| Revisión de 10:11 15 oct 2017 Coordinador (Discusión | contribuciones) (→Cálculo de los divisores de un número) ← Ir a diferencia anterior |
Revisión de 18:53 19 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | {{Caja_Amarilla|texto=Un número entero, {{Sube|porcentaje=+15%|contenido=<math>b\;</math>}}, es '''divisor''' de otro número entero, {{Sube|porcentaje=+10%|contenido=<math>a\;</math>}}, y lo expresaremos simbólicamente <math>b|a \;\!</math>, si la división de {{Sube|porcentaje=+10%|contenido=<math>a\;</math>}} entre {{Sube|porcentaje=+10%|contenido=<math>b\;</math>}} es exacta. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| + | *La división 60:15=4 es exacta. Entonces 15 es un divisor de 60 {{Sube|porcentaje=+15%|contenido=<math>(15|60 \;\!)</math>}}. | ||
| + | *Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas. | ||
| + | }} | ||
| {{Teorema_sin_demo|titulo=Propiedades de los divisores|enunciado= | {{Teorema_sin_demo|titulo=Propiedades de los divisores|enunciado= | ||
| *Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo. | *Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo. | ||
Revisión de 18:53 19 oct 2017
Un número entero, 
, es divisor de otro número entero, 
, y lo expresaremos simbólicamente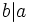 
, si la división de entre es exacta.
- La división 60:15=4 es exacta. Entonces 15 es un divisor de 60
.
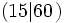- Fíjate que 4 también es divisor de 60 porque la división 60:4=15 es también exacta. Por tanto, los divisores siempre van por parejas.
Propiedades de los divisores
- Todo número natural distinto de cero tiene al menos dos divisores: 1 y él mismo.
- Todo divisor de un número distinto de cero es menor o igual a él. Por tanto, el número de divisores es finito.
- Si un número es divisor de otros dos, también lo es de su suma y de su diferencia.
- Si un número es divisor de otro, también lo es de cualquier múltiplo de éste.
- Si un número es divisor de otro, y éste lo es de un tercero, el primero lo es del tercero.
Cálculo de los divisores de un número
Procedimiento
Para encontar todos los divisores de un número, 
, buscamos las divisiones exactas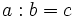 
. Entonces 
y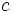 
son divisores de . Para ello procederemos de la siguiente manera:
- Probaremos con
.
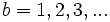- Para cada valor de que dé división exacta (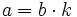
), tendremos dos divisores: y 
.
- Pararemos de probar cuando el cociente de la división
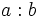sea menor o igual que .
Ejercicio resuelto: Cálculo de los divisores de un número
Calcula los divisores de 44.
44 : 1 = 44 
1 y 44 son divisores. Sigo porque 44 > 1
44 :2 = 22 2 y 22 son divisores. Sigo porque 22 > 2
44 : 3 No es exacta (cociente=14). Sigo porque 14 > 3
44 : 4 = 11 4 y 11 son divisores. Sigo porque 11 > 4
44 : 5 No es exacta (cociente=8). Sigo porque 8 > 5
44 : 6 No es exacta (cociente=7). Sigo porque 7 > 6
44 : 7 No es exacta (cociente=6). Paro porque 6 < 7
Ejercicio (4´44") Sinopsis:Calcula los divisores de 50 y de 60.
Divisores de un número Descripción: - Actividad que te muestra todos los divisores de un número dado.
- Actividad en la que debes averiguar todos los divisores de un numero dado.
- Actividad en la que debes separar los divisores de un número de los que no lo son.
Autoevaluación: Divisores de un número Descripción: Ejercicios de autoevaluación sobre divisores de un número.
Ejercicio 1 Descripción: Actividad en la que deberás hallar los divisores de un número.
Ejercicio 2 Descripción: Actividad en la que podrás calcular los divisores de un número.
Autoevaluación: Divisores Descripción: Ejercicios de autoevaluación sobre divisores de un número.
