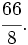Plantilla:Fracciones propias e impropias 1ºESO
De Wikipedia
| Revisión de 11:50 21 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:51 21 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 12: | Línea 12: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= |
| - | *'''Ejemplo 1:''' | + | '''Ejemplo 1:''' |
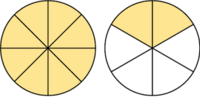
| La fracción {{b}}<math>\cfrac{10}{8}</math>{{b}} es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3): | La fracción {{b}}<math>\cfrac{10}{8}</math>{{b}} es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3): | ||
| <math>\cfrac{10}{8}= \cfrac{8}{8} + \cfrac{2}{8} = 1 +\cfrac{2}{8}</math> | <math>\cfrac{10}{8}= \cfrac{8}{8} + \cfrac{2}{8} = 1 +\cfrac{2}{8}</math> | ||
| - | + | <br> | |
| ---- | ---- | ||
| - | + | <br> | |
| - | *'''Ejemplo 2:''' | + | '''Ejemplo 2:''' |
| La frácción <math>\cfrac{35}{8}</math>es impropia. La podemosdecomponer en la suma de un entero y una fracción propia. | La frácción <math>\cfrac{35}{8}</math>es impropia. La podemosdecomponer en la suma de un entero y una fracción propia. | ||
| Línea 39: | Línea 39: | ||
| <center><math>\cfrac{35}{8}=4+\cfrac{3}{8}</math></center> | <center><math>\cfrac{35}{8}=4+\cfrac{3}{8}</math></center> | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 48: | Línea 49: | ||
| {{wolfram desplegable|titulo=Forma mixta de una fracción|contenido= | {{wolfram desplegable|titulo=Forma mixta de una fracción|contenido= | ||
| {{Wolfram forma mixta}} | {{Wolfram forma mixta}} | ||
| - | }} | ||
| }} | }} | ||
Revisión de 11:51 21 oct 2017
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Proposición Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como número mixto. Más concretamente, toda fracción impropia Demostración:
Ejemplo 1: La fracción
La frácción Para ello, dividimos 35 entre 8: 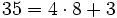 El dividendo Aplicando la proposición anterior: 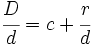 y sustituyendo cada letra por su valor: 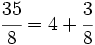 |
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 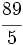
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 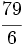
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 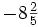
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
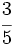 es una fracción propia porque 3 < 5.
es una fracción propia porque 3 < 5.
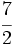 es una fracción impropia porque 7 > 2.
es una fracción impropia porque 7 > 2.
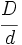 se puede escribir en la forma
se puede escribir en la forma 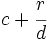 donde
donde  es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
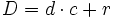
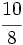 es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
es impropia. Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
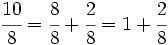
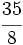 es impropia. La podemosdecomponer en la suma de un entero y una fracción propia.
es impropia. La podemosdecomponer en la suma de un entero y una fracción propia.
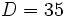 , el divisor
, el divisor 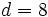 , el cociente
, el cociente 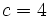 y el resto
y el resto 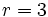 .
.
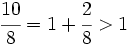
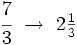 ; B)
; B) 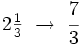
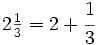
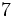

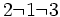 ; B)
; B)