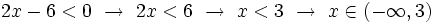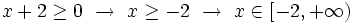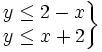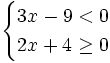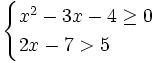Plantilla:Sistema de inecuaciones con una incógnita

De Wikipedia

(Diferencia entre revisiones)

Revisión de 16:53 29 oct 2017

Para resolver un sistema de inecuaciones con una incógnita, hay que resolver cada inecuación por separado y finalmente seleccionar la solución común a ambas (intersección de los conjuntos solución de ambas).

Resolución de sistemas de inecuaciones con una incógnita

Resuelve el siguiente sistema de inecuaciones:

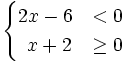
$\begin{cases} 2x-6 & < 0 \\ \; \, x+2 & \ge 0 \end{cases}$

Solución:

Resolvemos cada inecuación por separado:

$2x-6 < 0 \ \rightarrow \ 2x<6 \ \rightarrow \ x<3 \ \rightarrow \ x \in (- \infty, 3)$

$x+2 \ge 0 \ \rightarrow \ x \ge -2 \ \rightarrow \ x \in [-2, +\infty)$

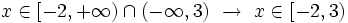
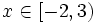
La solución común es la intersección de los conjuntos solución de ambas inecuaciones: $x \in [-2, +\infty) \cap (- \infty, 3) \ \rightarrow \ x \in [-2,3)$

Solución: $x \in [-2,3)$

Sistemas de inecuaciones lineales con una incógnita

Tutorial 1 (sist. inec. lineales) (5'09") Sinopsis:

Sistemas de inecuaciones de primer grado con una incógnita. Ejemplos.

Tutorial 2 (sist. inec. lineales o cuadráticas) (28'11") Sinopsis:

Todo lo que necesitas saber para resolver sistemas de inecuaciones (lineales o cuadráticas) de una variable. Tutorial que explica de forma completa la resolución de estos sistemas, resolviendo varios ejericios donde se aplica el algoritmo.

- 00:00 a 3:50: Definiciones y algoritmo de resolución.

- 3:50 a 28:11: Aplicación del algoritmo. Ejemplos resueltos.

Ejercicio 1 (5'49") Sinopsis:

Resuelve:

$\left . \begin{matrix} y \le 2-x \\ y \le x+2 \end{matrix} \right \}$

Ejercicio 2 (27'24") Sinopsis:

Resuelve:

a) 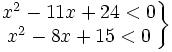$\left . \b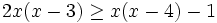egin{matrix} x^2-11x+24 < 0 \\ x^2-8x+15 < 0 \end{matrix} \right \}$

b) $2x(x-3) \ge x(x-4)-1\;$

Problema: Programación lineal (22'43") Sinopsis:

1 ejercicio.

Autoevaluación: Sistemas de inecuaciones lineales con una incógnita Descripción:

Autoevaluación sobre sistemas de inecuaciones lineales con una incógnita.

Sistemas de inecuaciones con una incógnita

Actividad: Sistemas de inecuaciones con una incógnita

Resuelve:

a) $\begin{cases} 3x-9<0 \\ 2x+4 \ge 0 \end{cases}$

b) $\begin{cases} x^2-3x-4 \ge 0 \\ 2x-7>5 \end{cases}$

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) 3x-9<0 ; 2x+4>=0 o bien solve 3x-9<0 ; 2x+4>=0

b) x^2-3x-4>=0, 2x-7>5

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Sistema_de_inecuaciones_con_una_inc%C3%B3gnita"

 |url1=http://www.unicoos.com/video/matematicas/2-bachiller/programacion-lineal/resolucion-de-problemas/programacion-lineal-01
 }}
 }}
+{{AI_vitutor
+|titulo1=Autoevaluación: ''Sistemas de inecuaciones lineales con una incógnita''
+|descripcion=Autoevaluación sobre sistemas de inecuaciones lineales con una incógnita.
+|url1=http://www.vitutor.com/ecuaciones/ine/ine02_Contenidos_e.html
+}}
 {{p}}
 {{wolfram desplegable|titulo=Sistemas de inecuaciones con una incógnita|contenido=

Plantilla:Sistema de inecuaciones con una incógnita

De Wikipedia

Revisión de 16:53 29 oct 2017

Vistas

Herramientas personales

Menú

Buscar

Herramientas