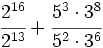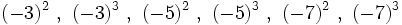Plantilla:Videos ejercicios propiedades potencias enteros
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:01 8 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 26: | Línea 26: | ||
| Calcula: | Calcula: | ||
| - | :a) <math>(-2)^4 \cdot (-2)^3\;</math> | + | :a) <math>(-2)^4 \cdot (-2)^3\;</math> ; {{b4}} b) <math>(-6)^9 : (-6)^4\;</math> |
| - | :b) <math>(-6)^9 : (-6)^4\;</math> | + | :c) <math>(-8)^2 \cdot (-8)^3\;</math> ; {{b4}} d) <math>(-2)^2 \cdot (-2)^3 \cdot (-2)\;</math> |
| - | :c) <math>(-8)^2 \cdot (-8)^3\;</math> | + | :e) <math>(-3)^7 : (-3)^4\;</math> ; {{b4}} f) <math>(-2)^5 \cdot (-2)^2\;</math> |
| - | :d) <math>(-2)^2 \cdot (-2)^3 \cdot (-2)\;</math> | + | :g) <math>(-7)^{12} : (-7)^{10}\;</math> ; {{b4}} h) <math>(-10)^3 : (-10)^2\;</math> |
| - | :e) <math>(-3)^7 : (-3)^4\;</math> | + | |
| - | :f) <math>(-2)^5 \cdot (-2)^2\;</math> | + | |
| - | :g) <math>(-7)^{12} : (-7)^{10}\;</math> | + | |
| - | :h) <math>(-10)^3 : (-10)^2\;</math> | + | |
| |url1=https://www.youtube.com/watch?v=RWCkyCK1Vw0&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B&index=4 | |url1=https://www.youtube.com/watch?v=RWCkyCK1Vw0&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B&index=4 | ||
| Línea 39: | Línea 35: | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| |titulo1=Ejercicio 2 | |titulo1=Ejercicio 2 | ||
| - | |duracion=7'58" | + | |duracion=12'23" |
| |sinopsis= | |sinopsis= | ||
| 10) Escribe en forma de una sola potencia: | 10) Escribe en forma de una sola potencia: | ||
| - | :a) <math>[(-2)^3]^5\;</math> | + | :a) <math>[(-2)^3]^5\;</math> ; {{b4}} b) <math>[(-3)^2]^3\;</math> |
| - | :b) <math>[(-3)^2]^3\;</math> | + | :c) <math>[(-5)^2]^4\;</math> ; {{b4}} d) <math>[(-6)^3]^3\;</math> |
| - | :c) <math>[(-5)^2]^4\;</math> | + | :e) <math>(2^4)^5\;</math> ; {{b4}} f) <math>(3^4)^2\;</math> |
| - | :d) <math>[(-6)^3]^3\;</math> | + | :g) <math>[(-2)^1]^6\;</math> ; {{b4}} h) <math>[(-2)^2]^6\;</math> |
| - | :e) <math>(2^4)^5\;</math> | + | :i) <math>(3^{10})^2\;</math> ; {{b4}} j) <math>(3^2)^{10}\;</math> |
| - | :f) <math>(3^4)^2\;</math> | + | |
| - | :g) <math>[(-2)^1]^6</math> | + | |
| - | :h) <math>[(-2)^2]^6\;</math> | + | |
| - | :i) <math>(3^{10})^2\;</math> | + | |
| - | :j) <math>(3^2})^{10}\;</math> | + | |
| 11) Expresa en forma de producto de varias potencias: | 11) Expresa en forma de producto de varias potencias: | ||
| - | :a) <math>[(-3) \cdot (-2) \cdot (-5)]^4</math> | + | :a) <math>[(-3) \cdot (-2) \cdot (-5)]^4\;</math> |
| - | :b) <math>[(-2) \cdot 5 \cdot (-6)]^2</math> | + | :b) <math>[(-2) \cdot 5 \cdot (-6)]^2\;</math> |
| - | :c) <math>[2 \cdot 7 \cdot 6]^3</math> | + | :c) <math>[2 \cdot 7 \cdot 6]^3\;</math> |
| - | :a) <math>[(-2) \cdot (-3) \cdot (-6)]^3</math> | + | :a) <math>[(-2) \cdot (-3) \cdot (-6)]^3\;</math> |
| 11) Expresa en forma de una sola potencia: | 11) Expresa en forma de una sola potencia: | ||
| - | :a) <math>(-2)^3 \cdot (-3)^3 \cdot (-4)^3</math> | + | :a) <math>(-2)^3 \cdot (-3)^3 \cdot (-4)^3\;</math> |
| - | :b) <math>(-2)^4 \cdot 3^4 </math> | + | :b) <math>(-2)^4 \cdot 3^4\; </math> |
| - | :c) <math>2^6 \cdot 4^6 \cdot 5^6</math> | + | :c) <math>2^6 \cdot 4^6 \cdot 5^6\;</math> |
| - | :d) <math>(-3)^6 \cdot (-10)^6</math> | + | :d) <math>(-3)^6 \cdot (-10)^6\;</math> |
| 12) Calcula los cuadrados de los cinco primeros números positivos. | 12) Calcula los cuadrados de los cinco primeros números positivos. | ||
| Línea 72: | Línea 63: | ||
| |url1=https://www.youtube.com/watch?v=sia5rDjOl28&index=5&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B | |url1=https://www.youtube.com/watch?v=sia5rDjOl28&index=5&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B | ||
| }} | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=10'07" | ||
| + | |sinopsis= | ||
| + | 14) Escribe las cuartas potencias de: -3, -2, -5, 3, 2 y 5. | ||
| + | |||
| + | 15) Calcula: | ||
| + | |||
| + | :a) <math>2 \cdot (-3)^2\;</math> ; {{b4}} b) <math>3 \cdot (-2)^2\;</math> | ||
| + | :c) <math>-1 \cdot (-3)^2\;</math> ; {{b4}} d) <math>-1 \cdot (-2)^2\;</math> | ||
| + | :e) <math>-2 \cdot (-3)^2\;</math> ; {{b4}} f) <math>-5 \cdot (-5)^2\;</math> | ||
| + | :g) <math>2 \cdot (-3)^2\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=f-BhbL-j9x8&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B&index=6 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 4 | ||
| + | |duracion=12'24" | ||
| + | |sinopsis= | ||
| + | 16) Escribe como potencias de base positiva: | ||
| + | |||
| + | : <math>(-3)^2 \ , \ (-3)^3 \ , \ (-5)^2 \ , \ (-5)^3 \ , \ (-7)^2 \ , \ (-7)^3\;</math> | ||
| + | |||
| + | 17) Escribe el resultado como potencia de base positiva: | ||
| + | |||
| + | :a) <math>(-5)^8 : (-5)^5\;</math> ; {{b4}} b) <math>(-10)^5 : (-10)^3\;</math> | ||
| + | :c) <math>(-20)^5 \cdot (-20)^3\;</math> ; {{b4}} d) <math>(-6)^2 \cdot 6^3\;</math> | ||
| + | :e) <math>(-3)^4 \cdot 3^2\;</math> ; {{b4}} f) <math>(-2)^5 \cdot 2^3\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=wqmn5kCiRt4&list=PLw7Z_p6_h3oyitluHq0d8ekp-ISvRvE4B&index=7 | ||
| + | }} | ||
| + | |||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Ejercicio 5 |
| |duracion=2'09" | |duracion=2'09" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>2 a^3 \cdot a^5</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>2 a^3 \cdot a^5</math>}} | ||
| Línea 79: | Línea 102: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 6 |
| |duracion=3'37" | |duracion=3'37" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left( \cfrac{5 \cdot 4 \cdot 3}{6 \cdot 2} \right)^2</math>}} | ||
| Línea 85: | Línea 108: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 7 |
| |duracion=3'42" | |duracion=3'42" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3</math>}} | ||
| Línea 91: | Línea 114: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 8 |
| |duracion=3'40" | |duracion=3'40" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{(3x^2y)^5}{3x^4y^7}</math>}} | ||
| Línea 97: | Línea 120: | ||
| }} | }} | ||
| {{Video_enlace_tuprofesorvirtual | {{Video_enlace_tuprofesorvirtual | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 9 |
| |duracion=2'47" | |duracion=2'47" | ||
| |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | |sinopsis=Simplifica: {{Sube|porcentaje=20%|contenido=<math>\cfrac{2^{16}}{2^{13}}+\cfrac{5^3 \cdot 3^8}{5^2 \cdot 3^6}</math>}} | ||
Revisión actual
Propiedades de las potencias y ejemplos:
- Potencias de exponente 0.
- Potencias de exponente 1.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
Propiedades de las potencias y ejemplos:
- Potencia de otra potencia.
- Potencia de un producto.
- Potencia de un cociente.
Calcula:
- a)
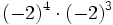 ; b)
; b) 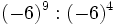
- c)
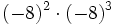 ; d)
; d) 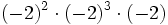
- e)
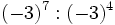 ; f)
; f) 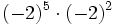
- g)
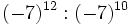 ; h)
; h) 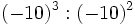
10) Escribe en forma de una sola potencia:
- a)
![[(-2)^3]^5\;](/wikipedia/images/math/8/8/6/886e30889b011f5f83334ec9296c0152.png) ; b)
; b) ![[(-3)^2]^3\;](/wikipedia/images/math/f/0/3/f037bb097909faad6873a0992df599fe.png)
- c)
![[(-5)^2]^4\;](/wikipedia/images/math/5/0/8/508d047dc4eb1a22b590a2f901a2fab9.png) ; d)
; d) ![[(-6)^3]^3\;](/wikipedia/images/math/4/c/8/4c8eef59c8fa17ac5bf2860de4ab42b4.png)
- e)
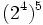 ; f)
; f) 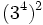
- g)
![[(-2)^1]^6\;](/wikipedia/images/math/d/f/3/df39089d6f5cc9c51e1d93713bb5f895.png) ; h)
; h) ![[(-2)^2]^6\;](/wikipedia/images/math/2/d/9/2d9edbe794a96dc0e0737db47be9067b.png)
- i)
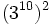 ; j)
; j) 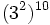
11) Expresa en forma de producto de varias potencias:
- a)
![[(-3) \cdot (-2) \cdot (-5)]^4\;](/wikipedia/images/math/3/2/6/3267df8521104f4db4a75cebb28001f7.png)
- b)
![[(-2) \cdot 5 \cdot (-6)]^2\;](/wikipedia/images/math/6/3/e/63e0b632e8c81875b6431d372a903f72.png)
- c)
![[2 \cdot 7 \cdot 6]^3\;](/wikipedia/images/math/1/a/0/1a083a19f18fa30e36b04f11289e2a1c.png)
- a)
![[(-2) \cdot (-3) \cdot (-6)]^3\;](/wikipedia/images/math/2/2/2/222cfc62f8027cac612dad7e3962dd04.png)
11) Expresa en forma de una sola potencia:
- a)
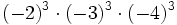
- b)
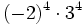
- c)
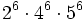
- d)
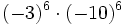
12) Calcula los cuadrados de los cinco primeros números positivos.
14) Escribe las cuartas potencias de: -3, -2, -5, 3, 2 y 5.
15) Calcula:
- a)
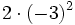 ; b)
; b) 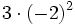
- c)
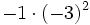 ; d)
; d) 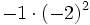
- e)
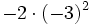 ; f)
; f) 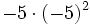
- g)
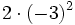
16) Escribe como potencias de base positiva:
17) Escribe el resultado como potencia de base positiva:
- a)
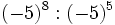 ; b)
; b) 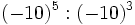
- c)
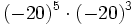 ; d)
; d) 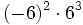
- e)
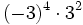 ; f)
; f) 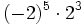
Simplifica: 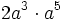
Simplifica: 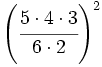
Simplifica: ![\left[ \cfrac{(8^2 \cdot 8) \cdot (6^7 \cdot 6)^2}{(8^3)^3 \cdot (6^3)^0 \cdot 6^3} \right]^3](/wikipedia/images/math/7/1/b/71b5b62cb54ed835ba335fdbca4de909.png)
Simplifica: 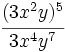
Simplifica: