Plantilla:Cálculo del máximo común divisor
De Wikipedia
| Revisión de 10:07 17 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:09 17 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 40: | Línea 40: | ||
| :Descomponemos 24 y 60 en sus factores primos:<br> | :Descomponemos 24 y 60 en sus factores primos:<br> | ||
| - | <center><math>24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5</math></center> | + | <center><math>24=2^3 \cdot 3 \qquad 60=2^2 \cdot 3 \cdot 5</math></center> |
| :Multiplicando los factores comunes elevados al menor exponente: | :Multiplicando los factores comunes elevados al menor exponente: | ||
| Línea 49: | Línea 49: | ||
| '''Calcula el m.c.d.(17,19) por el método óptimo''' | '''Calcula el m.c.d.(17,19) por el método óptimo''' | ||
| - | :Descomponemos 17 y 19 en sus factores primos:<br> | + | :Descomponemos 17 y 19 en sus factores:<br> |
| - | <center><math>17=17 \cdot 1\qquad 19=19 \cdot 1</math></center> | + | <center><math>17=17 \cdot 1 \qquad 19=19 \cdot 1</math></center> |
| :El único factor común es 1: | :El único factor común es 1: | ||
Revisión de 10:09 17 nov 2017
Procedimiento artesanal
Para calcular el máximo común divisor de dos o más números se siguen los siguientes pasos:
- Averiguaremos todos los divisores de dichos números.
- De los divisores comunes (los que se repitan en todos) cogeremos el mayor.
Calcula el m.c.d.(24,60) por el método artesanal
- Divisores de 24: 1, 2, 3, 4, 6, 8, 12, 24
- Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
- m.c.d.(24,60)= 12
Actividad en la que podrás ver como se obtiene el m.c.d de dos números mediante el procedimiento artesanal.
Procedimiento óptimo
Para obtener el m.c.d. de dos o más números se siguen los siguientes pasos:
- Se descomponen los números en factores primos.
- Se toman los factores comunes con menor exponente.
- Se multiplican dichos factores y el resultado obtenido es el m.c.d.
Nota: Cuando nos parezca que no hay ningún factor común, en realidad nos estamos olvidando del 1, que no es primo, pero es factor de cualquier número entero. Por tanto, si no hay coincidencia de ningún factor primo, el máximo común divisor es 1.
Calcula el m.c.d.(24,60) por el método óptimo
- Descomponemos 24 y 60 en sus factores primos:
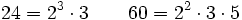
- Multiplicando los factores comunes elevados al menor exponente:
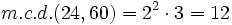
Calcula el m.c.d.(17,19) por el método óptimo
- Descomponemos 17 y 19 en sus factores:

- El único factor común es 1:
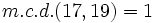
Tutorial que explica el significado del máximo común divisor, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los divisores de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 07:33: ¿Qué es el máximo común divisor? Método de extracción de divisores.
- 07:33 a 13:46: Método general para calcular el m.c.d. Ejemplos.
Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos o tres números.
Concepto y cálculo del máximo común divisor de dos o más números.
Concepto de máximo común divisor. Ejemplo.
Tutorial que explica qué es y cómo se calcula el máximo común divisor de dos números. Desarrolla un ejemplo en el que calcula el m.c.d. mediante el método artesanal.
Cálcula el máximo común divisor de 12 y 20
Cálcula el máximo común divisor de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Cálcula el máximo común divisor de:
a) 30 y 45
b) 36, 84 y 120
Cálcula el máximo común divisor de:
a) 18 y 24
b) 36, 54 y 90
Calcula:
- a) m.c.d.(36, 48).
- b) m.c.d.(60, 90, 150).
Calcula:
- a) m.c.d.(15, 20)
- b) m.c.d.(12, 18)
- c) m.c.d.(16, 20, 24)
- d) m.c.d.(18, 27)
Calcula:
- a) m.c.d.(8, 20)
- b) m.c.d.(96, 160, 24)
Calcula: m.c.d.(48, 36, 84).
Calcula: m.c.d.(72, 108, 60).
1) Calcula el m.c.d (-12, -30) hallando primero los divisores comunes.
2a) Calcula el m.c.d (6, -12) hallando primero los divisores comunes.
2b) Calcula el m.c.d (-12, -15) hallando primero los divisores comunes.
2c) Calcula el m.c.d (-6, 8) hallando primero los divisores comunes.
2d) Calcula el m.c.d (0, -18) hallando primero los divisores comunes.
2e) Calcula el m.c.d (6, 4) hallando primero los divisores comunes.
2f) Calcula el m.c.d (8, -72) hallando primero los divisores comunes.
3) Escribe los divisores de 4 y los divisores de 8.
- a) ¿Es 4 divisor de 8?
- b) ¿Son todos los divisores de 4 también divisores de 8?
- c) ¿Es 8 divisor de 4?
- d) ¿Son todos los divisores de 8 también divisores de 4?
- e) ¿Cuál es el m.c.d. de 4 y 8?
3) Calcula hallando los divisores comunes:
- a) m.c.d.(4, 16, 14)
- b) m.c.d.(9, 12, 18)
- c) m.c.d.(8, 16, 28)
- d) m.c.d.(21, 27, 30)
Ejercicios de autoevaluación sobre el m.c.d.
Juego para practicar el m.c.d.
Ejercicios de autoevaluación sobre el m.c.d. (Nivel avanzado)

