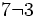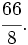Plantilla:Fracciones propias e impropias 1ºESO
De Wikipedia
| Revisión de 20:46 17 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 20:51 17 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Fracciones propias e impropias}} | {{Fracciones propias e impropias}} | ||
| + | {{p}} | ||
| + | ===Forma mixta de una fracción=== | ||
| + | {{Definición: número mixto}} | ||
| {{p}} | {{p}} | ||
| Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta. En efecto, fíjate en el siguiente resultado y el gráfico que lo acompaña. | Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta. En efecto, fíjate en el siguiente resultado y el gráfico que lo acompaña. | ||
| {{p}} | {{p}} | ||
| {{Tabla75|celda2=[[Imagen:fraccion_impropia.png|thumb|200px|Fig. 3: Para representar fracciones mayores que la unidad hay que utilizar más de un diagrama de tarta<center><math>\cfrac{10}{8}= 1 +\cfrac{2} {8} > 1</math></center>]]|celda1= | {{Tabla75|celda2=[[Imagen:fraccion_impropia.png|thumb|200px|Fig. 3: Para representar fracciones mayores que la unidad hay que utilizar más de un diagrama de tarta<center><math>\cfrac{10}{8}= 1 +\cfrac{2} {8} > 1</math></center>]]|celda1= | ||
| - | {{Teorema|titulo=Proposición|enunciado=Toda fracción impropia se puede expresar como un número entero más una fracción propia, es decir, como '''número mixto'''. | + | {{Teorema|titulo=Proposición: ''De de fracción impropia a forma mixta'' |
| + | |enunciado= | ||
| + | Toda fracción impropia, <math>\cfrac{D}{d}\;</math>, se puede escribir como suma de un número entero y una fracción propia. En consecuencia, toda fracción impropia se puede expresar en forma mixta: | ||
| + | {{b4}} | ||
| + | <center><math>\cfrac{D}{d}=c+\cfrac{r}{d}=c \begin{matrix} \frac{r}{d} \end{matrix}</math></center> | ||
| + | {{b4}} | ||
| + | |||
| + | donde <math>c\;\!</math> es el cociente y <math>r\;\!</math> es el resto de la división de <math>D\;\!</math> entre <math>d\;\!</math>. | ||
| + | |||
| - | Más concretamente, toda fracción impropia <math>\cfrac{D}{d}</math> se puede escribir en la forma <math>c+\cfrac{r}{d}</math> donde <math>c\;\!</math> es el cociente y <math>r\;\!</math> es el resto de la división de <math>D\;\!</math> entre <math>d\;\!</math>. | ||
| |demo= Basta aplicar el [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales:_Operaciones#Algoritmo_de_la_divisi.C3.B3n algoritmo de la división]: | |demo= Basta aplicar el [http://maralboran.ath.cx/wikipedia/index.php/N%C3%BAmeros_naturales:_Operaciones#Algoritmo_de_la_divisi.C3.B3n algoritmo de la división]: | ||
| <center><math>D=d \cdot c + r</math></center> | <center><math>D=d \cdot c + r</math></center> | ||
| y, a continuación, dividir todos los términos por <math>d\;\!</math> | y, a continuación, dividir todos los términos por <math>d\;\!</math> | ||
| <center><math>\cfrac{D}{d}=c+\cfrac{r}{d}</math></center> | <center><math>\cfrac{D}{d}=c+\cfrac{r}{d}</math></center> | ||
| - | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 20:51 17 nov 2017
¿Qué pasa si el numerador es mayor que el denominador? ¿Cómo se interpreta el hecho de tomar más partes de la unidad de las que que hay?
Vamos a dar respuesta a estas preguntas a continuación, pero primero necesitamos ver los conceptos de fracción propia e impropia.
- Fracciones propias son aquellas cuyo numerador (en valor absoluto) es menor que el denominador (en valor absoluto). Su valor absoluto es menor que 1.
- Fracciones impropias son aquellas que no son propias. Su valor absoluto es mayor que 1.
Representación gráfica de fracciones propias e impropias.
Actividad en la que debes separar las fracciones propias de las impropias
|
Actividad: Números racionales
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Forma mixta de una fracción
Una fracción mixta o número mixto es la representación de una fracción impropia como un número entero más una fracción propia, en la que se omite el signo de suma.
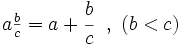
La fracción situada a la derecha del entero suele escribirse con una tipografía de menor tamaño para que no se confunda con una multiplicación de un número por una fracción.
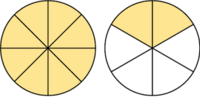
Las fracciones impropias representan algo mayor que el todo, es decir, cuando trabajamos con una fracción impropia damos a entender que tenemos unidades completas de algo y, posiblemente, alguna unidad incompleta. En efecto, fíjate en el siguiente resultado y el gráfico que lo acompaña.
Proposición: De de fracción impropia a forma mixta Toda fracción impropia, 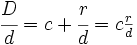
donde Demostración:
Ejemplo 1: La fracción Es mayor que la unidad y podemos expresarla como número mixto (Ver Fig. 3):
La frácción Para ello, dividimos 35 entre 8: 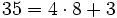 El dividendo Aplicando la proposición anterior: 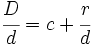 y sustituyendo cada letra por su valor: 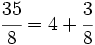 |
Números mixtos. Ejemplos de paso de forma fraccionaria a mixta y viceversa.
Conversión de fracción impropia a número mixto
Conversión de fracción impropia a número mixto.
Conversión de fracción impropia a número mixto.
Escribiendo una fracción impropia com un número mixto
Convierte a número mixto la siguiente fracción impropia: 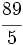
Nota: En el video, la división está realizada por el método anglosajón
Convierte a número mixto la siguiente fracción impropia: 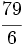
Nota: En el video, la división está realizada por el método anglosajón
Conversión de número mixto a fracción impropia
Conversión de número mixto a fracción impropia.
Conversión de número mixto a fracción impropia.
Convierte a fracción impropia el siguiente número mixto: 
Nota: En el video, la división está realizada por el método anglosajón
Convierte a fracción impropia el siguiente número mixto: 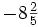
Nota: En el video, la división está realizada por el método anglosajón
Números mixtos y fracciones impropias.
Actividades de nivel variable en las que deberás obtener la forma mixta de una fracción.
|
Calculadora: Fracciones mixtas |
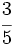 es una fracción propia porque 3 < 5.
es una fracción propia porque 3 < 5.
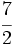 es una fracción impropia porque 7 > 2.
es una fracción impropia porque 7 > 2.
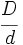 , se puede escribir como suma de un número entero y una fracción propia. En consecuencia, toda fracción impropia se puede expresar en forma mixta:
, se puede escribir como suma de un número entero y una fracción propia. En consecuencia, toda fracción impropia se puede expresar en forma mixta:
 es el cociente y
es el cociente y  es el resto de la división de
es el resto de la división de  entre
entre  .
.
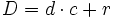
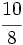 es impropia.
es impropia.
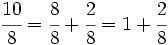
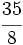 es impropia. La podemosdecomponer en la suma de un entero y una fracción propia.
es impropia. La podemosdecomponer en la suma de un entero y una fracción propia.
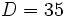 , el divisor
, el divisor 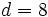 , el cociente
, el cociente 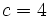 y el resto
y el resto 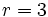 .
.
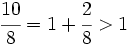
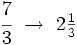 ; B)
; B) 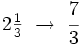
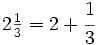

 ; B)
; B)