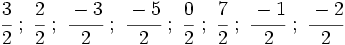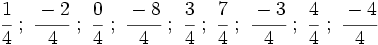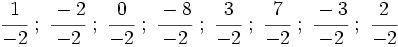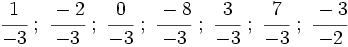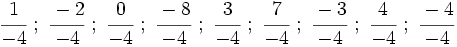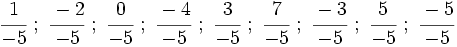Plantilla:Representación de fracciones en la recta numérica
De Wikipedia
| Revisión de 12:09 18 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Representación de fracciones en la recta numérica|enunciado= | {{Teorema_sin_demo|titulo=Representación de fracciones en la recta numérica|enunciado= | ||
| - | *Si la fracción representa un número entero (el cociente entre numerador y denominador es exacto), la representaremos tal. (Ver: [[El conjunto de los números enteros (1º ESO)|Números enteros]]). | + | *Si la fracción representa un número entero (el cociente entre numerador y denominador es exacto), la representaremos como tal. (Ver: [[El conjunto de los números enteros (1º ESO)|Números enteros]]). |
| *Si la fracción es '''propia''' y '''positiva''', se divide el segmento unidad de extremos 0 y 1, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la derecha, tantas de esas partes iguales como indique el numerador. | *Si la fracción es '''propia''' y '''positiva''', se divide el segmento unidad de extremos 0 y 1, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la derecha, tantas de esas partes iguales como indique el numerador. | ||
| *Si la fracción es '''propia''' y '''negativa''', se divide el segmento unidad de extremos -1 y 0, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la izquierda, tantas de esas partes iguales como indique el numerador. | *Si la fracción es '''propia''' y '''negativa''', se divide el segmento unidad de extremos -1 y 0, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la izquierda, tantas de esas partes iguales como indique el numerador. | ||
| Línea 13: | Línea 13: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_gris|texto=Para dividir un segmento en parte iguales podemos utilizar el Teorema de Thales. Puedes verlo en el siguiente video: | + | {{Nota|titulo=Sugerencia:|texto=Para dividir un segmento en parte iguales podemos utilizar el Teorema de Thales. Puedes verlo en el siguiente video: |
| {{Video_enlace_pdd | {{Video_enlace_pdd | ||
| Línea 33: | Línea 33: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Representación gráfica de las fracciones|enunciado= | + | {{Videotutoriales|titulo=Representación de fracciones en la recta numérica|enunciado= |
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| Línea 170: | Línea 170: | ||
| |descripcion=Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica. | |descripcion=Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_contenidos_1c.htm | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_contenidos_1c.htm | ||
| + | }} | ||
| + | {{AI_melide | ||
| + | |titulo1=Actividad 2 | ||
| + | |descripcion=Escribe la fracción impropia que corresponda a cada punto marcado en la recta. | ||
| + | |url1=http://maralboran.org/web_ma/Melide/Racionales_y_fracciones/Fracciones%20en%20la%20recta.html | ||
| }} | }} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás comprobar si sabes representar fracciones en la recta numérica. | |descripcion=En esta escena podrás comprobar si sabes representar fracciones en la recta numérica. | ||
| - | |enlace=[https://ggbm.at/z8ygsxHS Actividad 2] | + | |enlace=[http://ggbm.at/z8ygsxHS Actividad 3] |
| }} | }} | ||
| {{AI_descartes | {{AI_descartes | ||
| - | |titulo1=Actividad 3 | + | |titulo1=Actividad 4 |
| |descripcion= | |descripcion= | ||
| Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica: | Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica: | ||
Revisión actual
La representación de números enteros en la recta es algo muy sencillo. Como los enteros son "completos", la distancia entre dos consecutivos siempre es la misma, por lo que basta con escoger esa distancia para nuestra representación. Así, sí quisiésemos situar el número 7, por ejemplo, sólo tendríamos que contar siete saltos hacia la derecha desde el 0. Si quisiésemos representar un número negativo, los saltos serían hacia la izquierda del 0.
Sin embargo, para las fracciones no resulta tan sencillo, porque pueden representar cantidades que no son "completas" y hay que tener mucho cuidado con las distancias que se marcan.
Entonces, ¿cómo representamos una fracción en la recta? Para las fracciones propias es muy sencillo y para las impropias, basta con descomponerlas en parte entera más fracción propia.
Representación de fracciones en la recta numérica
- Si la fracción representa un número entero (el cociente entre numerador y denominador es exacto), la representaremos como tal. (Ver: Números enteros).
- Si la fracción es propia y positiva, se divide el segmento unidad de extremos 0 y 1, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la derecha, tantas de esas partes iguales como indique el numerador.
- Si la fracción es propia y negativa, se divide el segmento unidad de extremos -1 y 0, en tantas partes iguales como indique el denominador y contamos, desde el 0 hacia la izquierda, tantas de esas partes iguales como indique el numerador.
- Si la fracción es impropia y positiva, se expresa en la forma
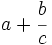 ("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
("valor entero" + "fracción propia") y dividimos el segmento de extremos a y a+1 en c partes iguales y contamos, desde el punto a, hacia la derecha, b de esas partes iguales.
- Si la fracción es impropia y negativa, se expresa en la forma
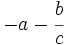 ("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
("-valor entero positivo" - "fracción propia de números positivos") y dividimos el segmento de extremos -(a+1) y -a en c partes iguales y contamos, desde el punto -a, hacia la izquierda, b de esas partes iguales.
Para dividir un segmento en parte iguales podemos utilizar el Teorema de Thales. Puedes verlo en el siguiente video:
En este vídeo aplicaremos el Teorema de Tales para dividir un segmento en partes iguales.
Ejemplo: Representación de fracciones en la recta numérica
Representa las fracciones:
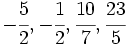
Nota: Pasa las fracciones impropias a forma mixta.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
Representación del conjunto de los racionales en la recta real.
Representación de fracciones en la recta numérica.
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Representa las siguientes fracciones en la recta numérica:
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Escribe la fracción que representa cada una de las letras representadas en la recta numérica.
Representa sobre la misma recta las fracciones 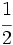 ,
, 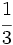 y
y 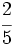 .
.
Representa sobre la misma recta las fracciones 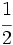 ,
, 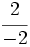 ,
, 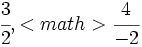 \;</math> y
\;</math> y 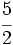 .
.
Representa sobre la misma recta las fracciones 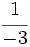 ,
, 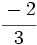 ,
, 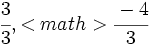 \;</math> y
\;</math> y 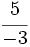 .
.
Representa en la recta real las fracciones 14/5 y -7/4.
Actividad en la que podrás ver como se representan gráficamente fracciones en la recta numérica.
Escribe la fracción impropia que corresponda a cada punto marcado en la recta.
En esta escena podrás comprobar si sabes representar fracciones en la recta numérica.
Haz en tu cuaderno la representación de las siguientes fracciones en la recta numérica:
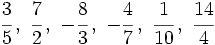
Compruéba las soluciones en la siguiente escena: