Plantilla:Division fracciones
De Wikipedia
| Revisión de 16:34 5 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja Amarilla| | + | {{Teorema_sin_demo|titulo=Procedimiento: ''División de fracciones''|enunciado= |
| - | texto= | + | Para '''dividir''' dos fracciones, se multiplica la primera fracción por la inversa de la segunda. |
| - | Para '''dividir''' dos fracciones, se pone como numerador, el producro del primer numerador por el segundo denominador, y como denominador, el producto del primer denominador por el segundo numerador. | + | |
| + | El resultado es otra fracción, cuyo numerador, es el producto del primer numerador por el segundo denominador, y cuyo denominador es el producto del primer denominador por el segundo numerador. | ||
| + | |||
| <center><math>\cfrac{a}{b} : \cfrac{c}{d}=\cfrac{a \cdot d}{b \cdot c}</math></center> | <center><math>\cfrac{a}{b} : \cfrac{c}{d}=\cfrac{a \cdot d}{b \cdot c}</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Observaciones:|texto= | ||
| + | #Si en una división de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad. | ||
| + | #La [[Números enteros: Múltiplicación y cociente (1º ESO)#División o cociente de números enteros|regla de los signos]] que utilizabamos para dividir números enteros sigue siendo válida con fracciones | ||
| + | |||
| + | }} | ||
| + | {{p}} | ||
| + | {{Warning|titulo=Advertencia:|texto=Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, al igual que ocurre con la multiplicación de fracciones, en ocasiones, podremos simplificar antes de efectuar los productos cruzados de los numeradores y denominadores. Lo que haremos es dejar indicados los productos cruzados y simplificarlos, si es posible, antes de multiplicarlos. Así ahorraras tiempo no teniendo que simplificar posteriormente. | ||
| }} | }} | ||
Revisión actual
Procedimiento: División de fracciones
Para dividir dos fracciones, se multiplica la primera fracción por la inversa de la segunda.
El resultado es otra fracción, cuyo numerador, es el producto del primer numerador por el segundo denominador, y cuyo denominador es el producto del primer denominador por el segundo numerador.
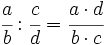
- Si en una división de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad.
- La regla de los signos que utilizabamos para dividir números enteros sigue siendo válida con fracciones
Es recomendable, al igual que con cualquier otra operación, simplificar el resultado final, sin embargo, al igual que ocurre con la multiplicación de fracciones, en ocasiones, podremos simplificar antes de efectuar los productos cruzados de los numeradores y denominadores. Lo que haremos es dejar indicados los productos cruzados y simplificarlos, si es posible, antes de multiplicarlos. Así ahorraras tiempo no teniendo que simplificar posteriormente.

