Plantilla:Ejemplos de uso del lenguaje algebraico
De Wikipedia
| Revisión de 11:02 22 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | Veamos algunas situaciones en la que tenemos que recurrir al lenguaje algebraico. | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| + | Veamos algunas situaciones en la que resulta conveniente recurrir al lenguaje algebraico: | ||
| + | |||
| *'''Expresión de propiedades o reglas''' | *'''Expresión de propiedades o reglas''' | ||
| Por ejemplo, la ''propiedad conmutativa del producto'' de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera: | Por ejemplo, la ''propiedad conmutativa del producto'' de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera: | ||
Revisión actual
Veamos algunas situaciones en la que resulta conveniente recurrir al lenguaje algebraico:
- Expresión de propiedades o reglas
Por ejemplo, la propiedad conmutativa del producto de dos números dice que "el orden de los factores no altera el producto". Ésto lo podemos expresar usando letras, de la siguiente manera:
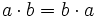
La regla de la división dice que "el dividendo es igual al divisor por el cociente más el resto". Ésto lo podemos expresar usando letras, de la siguiente manera:
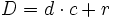
- Expresión de fórmulas
Por ejemplo, la fórmula del área del triángulo dice que "el área de un triángulo es igual a la base por la altura partido por 2", que podemos expresar con letras:
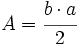
- Generalización de relaciones numéricas
Si consideramos la siguiente sucesión numérica
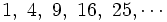
la expresión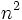 
sirve para generalizar sus términos, de manera que, si yo quiero obtener el término que ocupa el séptimo lugar, tan solo tendré que sustituir la letra 
por el número 7,
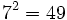
- Expresión de números desconocidos y planteamiento de ecuaciones
Por ejemplo, "la suma de dos números consecutivos es igual a 21" lo podemos expresar
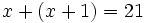
donde estamos utilizando la letra 
para representar al primer número y la expresión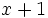 
para representar al segundo número.
