Plantilla:Def fraccion
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:49 19 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja Amarilla|texto=*Una '''fracción''' se expresa de la forma <math>\cfrac {a}{b}</math> con <math>a,b \in \mathbb{Z}</math>, donde <math>a\;\!</math> se llama '''numerador''' y <math>b\;\!</math> '''denominador'''. | + | {{concepto, significado y valor de una fracción}} |
| - | *El denominador indica las partes iguales en que se divide la unidad y el numerador las partes que tomamos de dicha división. | + | {{p}} |
| - | *El '''valor''' de una fracción es el resultado de dividir numerador entre denominador. | + | {{Videos definición fracción 3ºESO}} |
| - | *Una fracción puede ser: | + | |
| - | **Un '''número entero''': Si el resultado de hacer la división es exacto. | + | |
| - | **Un '''número fraccionario''': Si el resultado de hacer la división no es exacto. | + | |
| - | }} | + | |
Revisión actual
- Una fracción es una expresión de la forma
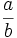 , o bien,
, o bien, 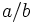 , donde
, donde  y
y  son números enteros, siendo
son números enteros, siendo 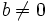 .
.
- Al número
 lo llamaremos numerador y al número
lo llamaremos numerador y al número  , denominador.
, denominador.
Una fracción se puede interpretar como una cantidad determinada de porciones que se toman de un todo dividido en partes iguales:
- El denominador sirve para representar las partes en que se divide la unidad.
- El numerador sirve para representar las porciones que tomamos.
El valor de una fracción es el resultado de dividir numerador entre denominador. Según su valor, una fracción pueden ser:
- Un número entero: Si el resultado de hacer la división es exacto.
- Un número fraccionario: Si el resultado de hacer la división no es exacto.
Esta definición nos da otra forma de interpretar a una fracción, ya que nos permite verla como una "división indicada" en las que el dividendo es el numerador y el cociente el denominador.
Tutorial que explica el concepto de fracción y su representación gráfica, en partes de la unidad y en la recta numérica.
- 00:00 a 04:14: Conceptos básicos. Ejemplos introductorios.
- 04:14 a 05:38: Definición matemática de fracción.
- 05:38 a 09:45: Representación de fracciones como partes de la unidad (Ejemplos).
- 09:45 a 19:26: Representación de fracciones en la recta numérica (Ejemplos).
- 11:25 a 13:45: Aplicación del Teorema de Tales para la división de segmentos en partes iguales.
- Definición de fracción.
- Fracciones equivalentes.
- Simplificación de fracciones. Fracciones irreducibles.
Clasificación de las fracciones:
- Fracciones propias e impropias.
- Fracciones ordinarias y decimales.
- Fracciones homogeneas y heterogeneas.
- Fracciones irreducibles y reducibles.

