Plantilla:Def cto racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:05 5 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:34 24 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| <center><math>\mathbb{Q} = \lbrace \cfrac {a}{b}\; / \; a,b \in \mathbb{Z}, \, b \ne 0 \rbrace</math></center> }} | <center><math>\mathbb{Q} = \lbrace \cfrac {a}{b}\; / \; a,b \in \mathbb{Z}, \, b \ne 0 \rbrace</math></center> }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_fonemato | ||
| + | |titulo1=Prohibido dividir por cero | ||
| + | |duracion=5'58" | ||
| + | |sinopsis=Todo cociente de números cuyo denominador sea 0 carece de sentido matemático. | ||
| + | De otro modo: si se admite la división por "cero" es el caos, pues entonces 2 = 1. Por eso,si divides por cero, aunque sea sin darte cuenta, serás fusilado de inmediato y expulsado de la comunidad científica por los siglos de los siglos. | ||
| + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/05-prohibido-dividir-por-cero-4#.VCVbhhZ8HA8 | ||
| + | }} | ||
Revisión de 10:34 24 nov 2017
El conjunto de los números racionales es el conjunto de todas las fracciones:
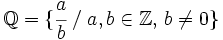
Prohibido dividir por cero (5'58") Sinopsis: Todo cociente de números cuyo denominador sea 0 carece de sentido matemático. De otro modo: si se admite la división por "cero" es el caos, pues entonces 2 = 1. Por eso,si divides por cero, aunque sea sin darte cuenta, serás fusilado de inmediato y expulsado de la comunidad científica por los siglos de los siglos.
