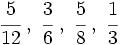Plantilla:Ordenar fracciones
De Wikipedia
| Revisión de 10:48 19 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:18 27 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. Vamos a ver otro procedimiento que consiste en reducirlas a común denominador. | + | Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división. |
| + | {{p}} | ||
| + | En algunos casos es fácil comparar dos fracciones sin necesidad de hacer la división. | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Ordenar fracciones|enunciado= | ||
| + | *De dos fracciones con el mismo denominador, es mayor la de mayor numerador. | ||
| + | *De dos fracciones con el mismo numerador, es mayor la de menor denominador. | ||
| + | }} | ||
| + | {{p}} | ||
| + | Veamos ahora un procedimiento para los casos en que no sean iguales ni los numeradores ni los denominadores. Lo que haremos será reducirlas a común denominador. | ||
| {{p}} | {{p}} | ||
| [[Imagen:Red_comun_den.gif|center]] | [[Imagen:Red_comun_den.gif|center]] | ||
| Línea 6: | Línea 15: | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Ordenar fracciones|enunciado=*Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador. | {{Teorema_sin_demo|titulo=Ordenar fracciones|enunciado=*Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador. | ||
| - | *De dos fracciones con el mismo denominador, es mayor la de mayor numerador. | + | *Una vez reducidas a común denominador, será mayor la de mayor numerador. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:18 27 nov 2017
Una forma de comparar fracciones consistía en calcular su valor numérico, efectuando la división.
En algunos casos es fácil comparar dos fracciones sin necesidad de hacer la división.
Ordenar fracciones
- De dos fracciones con el mismo denominador, es mayor la de mayor numerador.
- De dos fracciones con el mismo numerador, es mayor la de menor denominador.
Veamos ahora un procedimiento para los casos en que no sean iguales ni los numeradores ni los denominadores. Lo que haremos será reducirlas a común denominador.
En la animación anterior, cuando los denominadores son distintos, no podemos comparar las piezas coloreadas de verde, pues son de tamaños distintos. Al cambiar los denominadores por 12, sí podemos hacer la comparación. Además, 12 no es un denominador cualquiera, es el mínimo común múltiplo de 3 y 4. Se podría usar cualquier otro múltiplo común, pero lo normal es usar el menor posible para no trabajar con números muy grandes.
Ordenar fracciones
- Para ordenar fracciones con distinto denominador debemos primero reducirlas a común denominador.
- Una vez reducidas a común denominador, será mayor la de mayor numerador.
Ejemplo: Ordenar fracciones
Ordena las siguientes fracciones: 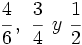
Calculamos el m.c.m. de los denominadores:
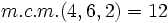 .
.
A continuación, las reducimos a común denominador:
Nótese que hemos multiplicado numerador y denominador por el resultado de dividir el m.c.m. , 12, por cada denominador.
Ordenamos las fracciones obtenidas, y a partir de ellas las fracciones de partida:
Ordena las siguientes fracciones:
a) 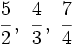
b) 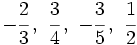
b) 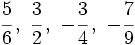
Comparación de fracciones. Ordenar fracciones de forma ascendente. Atención al método usado para obtener el m.c.m. Ordenar fracciones de forma descendente. Compara Compara | Compara Compara Compara Compara |
Actividad en la que podrás ver como se comparan fracciones reduciéndolas a común denominador, tanto si son positivas como negativas.
Actividad en la que debes ordenas varias fracciones.
Actividad en la deberás comparar fracciones.
Actividad en la deberás comparar fracciones.
Ordena fracciones.
Ejercicios de autoevaluación sobre ordenación y comparación de fracciones.
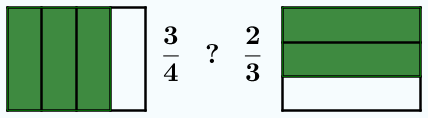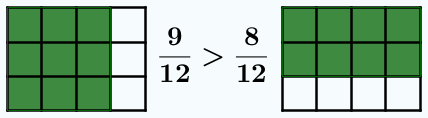
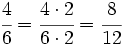
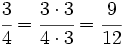
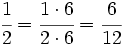
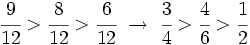
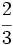 y
y 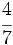 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
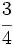 y
y 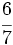 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
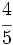 y
y 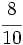 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
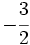 y
y 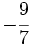 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
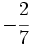 y
y 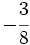 mediante la comparación de los productos cruzados.
mediante la comparación de los productos cruzados.
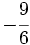 y
y