Plantilla:Simplificación de fracciones
De Wikipedia
| Revisión de 08:33 19 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja Amarilla|texto='''Simplificar una fracción''' consiste en obtener otra fracción equivalente con numerador y denominador menores que los de partida. | + | {{Caja_Amarilla|texto=*'''Simplificar''' una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida. |
| - | *Para ello debemos dividir numerador y denominador por un mismo número. | + | *Cuando una fracción no se puede simplificar se dice que es '''irreducible'''.}} |
| - | *Este proceso se puede repetir hasta que ya no encontremos más divisores comunes distintos de 1, en cuyo caso, la fracción así obtenida se dice que es '''irreducible'''.}} | + | {{p}} |
| + | {{Teorema_sin_demo|titulo=Procedimiento: ''Simplificación''|enunciado=*Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible. | ||
| + | *Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.}} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| + | Simplifica <math>\cfrac{24}{30}</math>: | ||
| + | ---- | ||
| + | '''Solución:''' | ||
| + | |||
| + | *'''Paso a paso:''' Dividimos por 2 y luego por 3 | ||
| + | {{p}} | ||
| + | :<math>\cfrac{24}{30} = \cfrac{12}{15} = \cfrac{4}{5}</math> | ||
| + | {{p}} | ||
| + | *'''En un solo paso:''' Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6: | ||
| + | {{p}} | ||
| + | :<math>\cfrac{24}{30} = \cfrac{4}{5}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videos: Ejercicios de simplificación de fracciones}} | ||
| + | {{p}} | ||
| + | {{Actividades simplificar fracciones}} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Simplificación de fracciones|contenido= | ||
| + | {{Wolfram simplificar fracciones}} | ||
| + | }} | ||
| + | {{p}} | ||
| + | La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes. | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.}} | ||
| + | {{p}} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejemplo | ||
| + | |duracion=5'07" | ||
| + | |sinopsis=Determina si <math>\cfrac{30}{45}</math> y <math>\cfrc{54}{81}</math> son fracciones equivalentes. | ||
| + | |url1=https://www.youtube.com/watch?v=5qyHfhLLkvs | ||
| + | }} | ||
Revisión actual
- Simplificar una fracción es sustituirla por otra equivalente con el numerador y denominador menores que los de partida.
- Cuando una fracción no se puede simplificar se dice que es irreducible.
Procedimiento: Simplificación
- Para simplificar fracciones se divide numerador y denominador por un mismo número, distinto de 0 y 1. Este proceso se puede repetir hasta hacer la fracción irreducible.
- Si queremos hacer la fracción irreducible en un solo paso debemos dividir numerador y denominador por el m.c.d. de ambos.
Simplifica 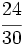 :
:
Solución:
- Paso a paso: Dividimos por 2 y luego por 3
- En un solo paso: Calculamos el m.c.d.(24,30) = 6, y dividimos directamente por 6:
Simplificación de fracciones (3 métodos). Fracción irreducible. Ejemplos.
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica:
Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: Simplifica: | Simplifica: Simplifica: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: Halla la fracción irreducible de: |
- Actividades en las que deberás simplificar fracciones con o sin ayuda.
- Actividad en la que debes emparejar cada fracción con su irreducible.
Actividad en las que deberás encontrar la fracción irreducible.
Actividades de nivel variable en las que deberás simplificar fracciones.
Simplifica fracciones.
La simplificación de fracciones me proporciona un método para saber si dos fracciones son equivalentes.
Procedimiento
Si al simplificar dos fracciones se obtiene la misma fracción irreducible, entonces las dos fracciones son equivalentes.
Determina si 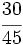 y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
y No se pudo entender (función desconocida\cfrc): \cfrc{54}{81}
son fracciones equivalentes.
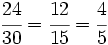
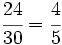
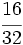 b)
b) 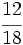
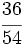 b)
b) 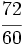
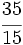 b)
b) 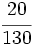
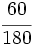 b)
b) 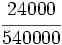
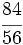 b)
b) 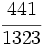
 b)
b) 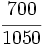
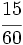
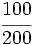 .
.
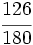 .
.
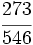 .
.
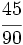 .
.
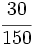 .
.
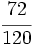 .
.
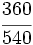 .
.
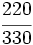 .
.
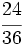 .
.
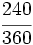 .
.
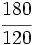 .
.
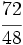 .
.
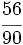 .
.
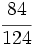 .
.
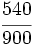 .
.
 .
.
 .
.