Plantilla:Paso de fraccion a decimal
De Wikipedia
| Revisión de 08:01 7 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Tipos de expresiones decimales de una fracción) |
||
| Línea 1: | Línea 1: | ||
| - | Para pasar de fracción a decimal basta con hacer la división del numerador entre el denominador. Pueden darse los siguientes casos, según sea la expresión decimal resultante:{{p}} | + | {{Paso de fracción a decimal 1ºESO}} |
| - | {{Caja Amarilla|texto= | + | {{p}} |
| + | ===Tipos de expresiones decimales de una fracción=== | ||
| + | {{Caja Amarilla|texto=La expresión decimal de una fracción puede ser: | ||
| + | |||
| *'''Expresión decimal exacta:''' Si tiene un número finito de decimales. | *'''Expresión decimal exacta:''' Si tiene un número finito de decimales. | ||
| - | :Por ejemplo: <math>\cfrac{7}{16}=0,4375</math>. | + | |
| *'''Expresión decimal periódica pura:''' Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama '''periodo'''. | *'''Expresión decimal periódica pura:''' Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama '''periodo'''. | ||
| - | :Por ejemplo: <math>\cfrac{6}{11}=0,545454...=0,\widehat{54}</math>. El periodo es 54. | + | |
| *'''Expresión decimal periódica mixta:''' Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama '''periodo''' y la parte decimal previa al periodo se llama '''anteperiodo'''. | *'''Expresión decimal periódica mixta:''' Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama '''periodo''' y la parte decimal previa al periodo se llama '''anteperiodo'''. | ||
| - | :Por ejemplo: <math>\cfrac{4}{15}=0,266666...=0,2\widehat{6}</math>. El periodo es 6 y el anteperiodo 2. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI_cidead | + | {{Nota: tipos de expresiones decimales}} |
| - | |titulo1=Paso de fracción a decimal | + | {{p}} |
| - | |descripcion=#Actividad en la que podrás ver como se obtiene la expresión decimal de una fracción viendo el desarrollo de la división y los decimales que se obtienen en el cociente. | + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= |
| - | #Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena. | + | *'''Decimal exacto:'''{{b}} <math>\cfrac{53}{4}=13.25 \ ; \quad \cfrac{52}{100}=0.52</math> |
| + | |||
| + | *'''Decimal periódico puro:'''{{b}} <math>\cfrac{2}{3}=0.6666...=0.\widehat{6}</math>{{b4}}(El periodo es 6) | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena1/3quincena1_contenidos_1a.htm | + | *'''Decimal periódico mixto:'''{{b}} <math>\cfrac{5}{6}=0.8333...=0.8\widehat{3}</math>{{b4}}(El anteperiodo es 8 y el periodo es 3) |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Videos:Paso de fracción a decimal}} | {{Videos:Paso de fracción a decimal}} | ||
| + | {{Actividad: Paso de fracción a decimal}} | ||
Revisión actual
Aunque una fracción es un valor exacto y los números decimales a veces requieren tomar aproximaciones, muchas veces resulta más cómodo trabajar con decimales que con fracciones.
Procedimiento
Una fracción se puede expresar como un número decimal calculando su valor, es decir, dividiendo numerador entre denominador.
Tipos de expresiones decimales de una fracción
La expresión decimal de una fracción puede ser:
- Expresión decimal exacta: Si tiene un número finito de decimales.
- Expresión decimal periódica pura: Si tiene un número infinito de decimales que se repiten. La parte que se repite se llama periodo.
- Expresión decimal periódica mixta: Si tiene un número infinito de decimales que se repiten a partir de una cierta posición decimal. La parte que se repite se llama periodo y la parte decimal previa al periodo se llama anteperiodo.
"El número decimal que resulta de dividir el numerador de una fracción entre su denominador es siempre exacto o periódico".
En efecto, piensa en el algoritmo de la división. Si tenemos la suerte de llegar a resto 0, el cociente será un decimal exacto. Si, por el contrario, no conseguimos que el resto sea 0, podemos bajar ceros del dividendo tantas veces como queramos. El asunto es que los restos que pueden aparecer en cada paso tienen que ser menores que el divisor, por tanto, hay un número limitado de restos posibles. Por ejemplo, si dividimos entre 4, los restos podrían ser 0, 1, 2 o 3. Entonces, si seguimos dividiendo (bajando ceros) y no conseguimos que el resto sea cero, en algún momento tendrá que repetirse un resto de entre todos los posibles y el cociente será un decimal periódico.
- Decimal exacto:

- Decimal periódico puro:
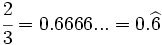 (El periodo es 6)
(El periodo es 6)
- Decimal periódico mixto:
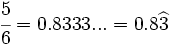 (El anteperiodo es 8 y el periodo es 3)
(El anteperiodo es 8 y el periodo es 3)
Cómo obtener la expresión decimal de una fracción. Ejemplos:
1. a) 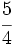 b)
b) 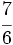
2. a) 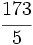 b)
b) 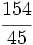 c)
c) 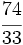
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de una fracción a su expresión decimal equivalente (finito o periódico).
Obtén la expresión decimal de 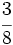
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 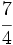
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 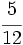
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 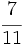
Nota: En el video, la división está realizada por el método anglosajón
Obtén la expresión decimal de 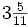
Nota: En el video, la división está realizada por el método anglosajón
Transforma en decimales las siguientes fracciones:
a) 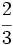 ; b)
; b) 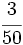 ; c)
; c) 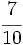 ; d)
; d) 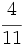 ; e)
; e) 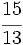
Transforma en decimales las siguientes fracciones:
a) 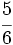 ; b)
; b) 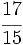 ; c)
; c) 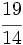 ; d)
; d) 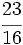
Transforma en decimales las siguientes fracciones decimales:
a) 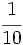 ; b)
; b) 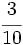 ; c)
; c) 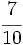 ; d)
; d) 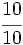 ; e)
; e) 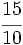 ;
;
f) 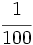 ;g)
;g) 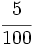 ; h)
; h) 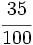 ; i)
; i) 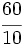 ; j)
; j) 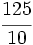 ;
;
k) 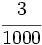 ; l)
; l) 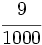 ; m)
; m) 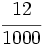 ; n)
; n) 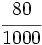 ; o)
; o) 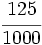 ; p)
; p) 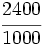
- Actividad en la que podrás ver como se obtiene la expresión decimal de una fracción viendo el desarrollo de la división y los decimales que se obtienen en el cociente.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
- Fracciones con expresiones decimales exactas.
- Actividad en la que tendrás que elegir qué tipo de expresión decimal es la que te muestran en la escena.
Convertir fracciones a decimales.

