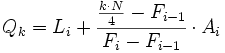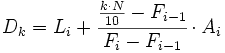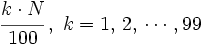Plantilla:Parámetros de posición
De Wikipedia
| Revisión de 09:04 6 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:14 5 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Los '''parámetros de posición''' dividen un conjunto de datos ordenados en grupos con el mismo número de individuos. Son los siguientes: | + | Los '''parámetros de posición''' dividen un conjunto de datos ordenados en grupos con el mismo número de individuos. Hay tres tipos: cuartiles, deciles y percentiles. |
| - | + | }} | |
| - | *'''Cuartiles:''' Son los valores de la variable que dividen la serie ordenada de datos en cuatro partes iguales. | + | {{p}} |
| - | **Los cuartiles son tres: Q<sub>1</sub>, Q<sub>2</sub> y Q<sub>3</sub>, que delimitan al 25%, al 50% y al 75% de los datos, respectivamente. | + | ===Cuartiles=== |
| - | **Q<sub>2</sub> coincide con la mediana. | + | {{Caja_Amarilla|texto= |
| - | **La diferencia Q<sub>3</sub> - Q<sub>1</sub> se llama '''recorrido intercuartílico'''. | + | Los '''cuartiles''' son los valores de la variable que dividen la serie ordenada de datos en cuatro partes iguales. |
| - | + | *Los cuartiles son tres: Q<sub>1</sub>, Q<sub>2</sub> y Q<sub>3</sub>, que delimitan al 25%, al 50% y al 75% de los datos, respectivamente. | |
| - | *'''Deciles:''' Son los valores de la variable que dividen la serie ordenada de datos en diez partes iguales. | + | *Q<sub>2</sub> coincide con la mediana. |
| - | **Los deciles son 9: D<sub>1</sub>, D<sub>2</sub> ... , D<sub>9</sub>, que delimitan al 10%, al 20%, ..., 90% de los datos, respectivamente. | + | *La diferencia Q<sub>3</sub> - Q<sub>1</sub> se llama '''recorrido intercuartílico'''. |
| - | **D<sub>5</sub> coincide con la mediana. | + | |
| - | *'''Percentiles:''' Son los valores de la variable que dividen la serie ordenada de datos en cien partes iguales. | + | |
| - | **Los percentiles son 99: P<sub>1</sub>, P<sub>2</sub> ... , P<sub>99</sub>, que delimitan al 1%, al 2%, ... , 99% de los datos, respectivamente. | + | |
| - | **P<sub>50</sub> coincide con la mediana. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Cálculo de los parámetros de posición|enunciado= | + | {{Teorema_sin_demo|titulo=Cálculo de los cuartiles|enunciado= |
| - | Para calcular los parámetros de posición es necesario que los N datos estén ordenados de menor a mayor. | + | Para calcular los cuartiles es necesario que los N datos estén ordenados de menor a mayor. |
| - | *'''Cuartiles:''' Procederemos como hacíamos con la mediana, pero ahora buscaremos el lugar que ocupa cada cuartil mediante la expresión | + | Procederemos como hacíamos con la mediana, pero ahora buscaremos el lugar que ocupa cada cuartil mediante la expresión |
| <center><math>\cfrac{k \cdot N}{4} \, , \ k=1,\, 2,\, 3</math></center> | <center><math>\cfrac{k \cdot N}{4} \, , \ k=1,\, 2,\, 3</math></center> | ||
| Línea 35: | Línea 31: | ||
| ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el cuartil. | ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el cuartil. | ||
| ::*<math>N\;</math> es el número de datos. | ::*<math>N\;</math> es el número de datos. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Cuartiles | ||
| + | |descripcion=Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística. | ||
| + | |||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3c.htm | ||
| + | }} | ||
| {{Web_enlace_vitutor | {{Web_enlace_vitutor | ||
| |descripcion=Cuartiles. Ejemplos. | |descripcion=Cuartiles. Ejemplos. | ||
| Línea 45: | Línea 48: | ||
| |titulo1=Ejercicios resueltos: ''Cuartiles'' | |titulo1=Ejercicios resueltos: ''Cuartiles'' | ||
| }} | }} | ||
| - | ---- | + | {{p}} |
| - | *'''Deciles:''' Procederemos como antes, pero buscaremos el lugar que ocupa cada decil mediante la expresión | + | ===Deciles=== |
| + | {{Caja_Amarilla|texto= | ||
| + | Los '''deciles''' son los valores de la variable que dividen la serie ordenada de datos en diez partes iguales. | ||
| + | *Los deciles son 9: D<sub>1</sub>, D<sub>2</sub> ... , D<sub>9</sub>, que delimitan al 10%, al 20%, ..., 90% de los datos, respectivamente. | ||
| + | *D<sub>5</sub> coincide con la mediana. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Cálculo de los deciles|enunciado= | ||
| + | Para calcular los deciles es necesario que los N datos estén ordenados de menor a mayor. | ||
| + | |||
| + | Procederemos como antes, pero buscaremos el lugar que ocupa cada decil mediante la expresión | ||
| <center><math>\cfrac{k \cdot N}{10} \, , \ k=1,\, 2,\, \cdots , 9</math></center> | <center><math>\cfrac{k \cdot N}{10} \, , \ k=1,\, 2,\, \cdots , 9</math></center> | ||
| Línea 61: | Línea 74: | ||
| ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el decil. | ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el decil. | ||
| ::*<math>N\;</math> es el número de datos. | ::*<math>N\;</math> es el número de datos. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Web_enlace_vitutor | {{Web_enlace_vitutor | ||
| Línea 71: | Línea 85: | ||
| |titulo1=Ejercicios resueltos: ''Deciles'' | |titulo1=Ejercicios resueltos: ''Deciles'' | ||
| }} | }} | ||
| - | ---- | + | {{p}} |
| - | *'''Percentiles:''' Procederemos como antes, pero buscaremos el lugar que ocupa cada percentil mediante la expresión | + | ===Percentiles=== |
| + | {{Caja_Amarilla|texto= | ||
| + | Los '''percentiles''' son los valores de la variable que dividen la serie ordenada de datos en cien partes iguales. | ||
| + | *Los percentiles son 99: P<sub>1</sub>, P<sub>2</sub> ... , P<sub>99</sub>, que delimitan al 1%, al 2%, ... , 99% de los datos, respectivamente. | ||
| + | *P<sub>50</sub> coincide con la mediana. | ||
| + | }} | ||
| + | {{p}} | ||
| + | |||
| + | {{Teorema_sin_demo|titulo=Cálculo de los percentiles|enunciado= | ||
| + | Para calcular los percentiles es necesario que los N datos estén ordenados de menor a mayor. | ||
| + | |||
| + | Procederemos como antes, pero buscaremos el lugar que ocupa cada percentil mediante la expresión | ||
| {{caja|contenido=<math>\cfrac{k \cdot N}{100} \, , \ k=1,\, 2,\, \cdots , 99</math>}} | {{caja|contenido=<math>\cfrac{k \cdot N}{100} \, , \ k=1,\, 2,\, \cdots , 99</math>}} | ||
| Línea 87: | Línea 112: | ||
| ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el percentil. | ::*<math>A_i\;</math> es la amplitud del intervalo donde se halla el percentil. | ||
| ::*<math>N\;</math> es el número de datos. | ::*<math>N\;</math> es el número de datos. | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{Web_enlace_vitutor | {{Web_enlace_vitutor | ||
| Línea 96: | Línea 122: | ||
| |url1=http://www.vitutor.com/estadistica/descriptiva/d_9.html | |url1=http://www.vitutor.com/estadistica/descriptiva/d_9.html | ||
| |titulo1=Ejercicios resueltos: ''Percentiles'' | |titulo1=Ejercicios resueltos: ''Percentiles'' | ||
| - | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ---- | ||
| {{Web_enlace | {{Web_enlace | ||
| |descripcion=En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se calculan los parámetros de posición. | |descripcion=En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se calculan los parámetros de posición. | ||
| - | |enlace=[https://www.portaleducativo.net/octavo-basico/830/Medidas-de-posicion Ejemplos: ''Parámetros de posición''] | + | |enlace=[http://www.portaleducativo.net/octavo-basico/830/Medidas-de-posicion Parámetros de posición] |
| - | }} | + | |
| - | {{AI_cidead | + | |
| - | |titulo1=Cuartiles | + | |
| - | |descripcion=Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística. | + | |
| - | + | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena11/3quincena11_contenidos_3c.htm | + | |
| }} | }} | ||
| {{Videotutoriales|titulo=Cálculo de los parámetros de posición|enunciado= | {{Videotutoriales|titulo=Cálculo de los parámetros de posición|enunciado= | ||
Revisión de 12:14 5 dic 2017
Los parámetros de posición dividen un conjunto de datos ordenados en grupos con el mismo número de individuos. Hay tres tipos: cuartiles, deciles y percentiles.
Tabla de contenidos |
Cuartiles
Los cuartiles son los valores de la variable que dividen la serie ordenada de datos en cuatro partes iguales.
- Los cuartiles son tres: Q1, Q2 y Q3, que delimitan al 25%, al 50% y al 75% de los datos, respectivamente.
- Q2 coincide con la mediana.
- La diferencia Q3 - Q1 se llama recorrido intercuartílico.
Cálculo de los cuartiles
Para calcular los cuartiles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como hacíamos con la mediana, pero ahora buscaremos el lugar que ocupa cada cuartil mediante la expresión

- en lugar del valor que usábamos para la mediana,
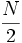 . (Fíjate que para k=2 se obtiene precisamente dicho valor, ya que Q2 es la mediana)
. (Fíjate que para k=2 se obtiene precisamente dicho valor, ya que Q2 es la mediana)
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
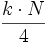 se redondea al siguiente número entero, y el dato ocupe dicho lugar será el cuartil.
se redondea al siguiente número entero, y el dato ocupe dicho lugar será el cuartil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
|
|
- donde:
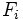 es la frecuencia acumulada del intervalo donde se encuentra el cuartil y
es la frecuencia acumulada del intervalo donde se encuentra el cuartil y 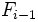 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 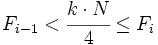 .
.
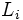 es el límite inferior del intervalo donde se halla el cuartil.
es el límite inferior del intervalo donde se halla el cuartil.
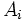 es la amplitud del intervalo donde se halla el cuartil.
es la amplitud del intervalo donde se halla el cuartil.
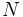 es el número de datos.
es el número de datos.
Actividades en la que podrás aprender a calcular los cuartiles de una distribución estadística.
Cuartiles. Ejemplos.
Ejercicios resueltos sobre cuartiles.
Deciles
Los deciles son los valores de la variable que dividen la serie ordenada de datos en diez partes iguales.
- Los deciles son 9: D1, D2 ... , D9, que delimitan al 10%, al 20%, ..., 90% de los datos, respectivamente.
- D5 coincide con la mediana.
Cálculo de los deciles
Para calcular los deciles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como antes, pero buscaremos el lugar que ocupa cada decil mediante la expresión
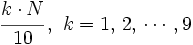
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
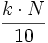 se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el decil.
se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el decil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
|
|
- donde:
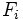 es la frecuencia acumulada del intervalo donde se encuentra el decil y
es la frecuencia acumulada del intervalo donde se encuentra el decil y 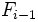 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 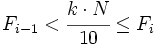 .
.
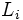 es el límite inferior del intervalo donde se halla el decil.
es el límite inferior del intervalo donde se halla el decil.
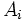 es la amplitud del intervalo donde se halla el decil.
es la amplitud del intervalo donde se halla el decil.
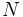 es el número de datos.
es el número de datos.
Deciles. Ejemplos.
Ejercicios resueltos sobre deciles.
Percentiles
Los percentiles son los valores de la variable que dividen la serie ordenada de datos en cien partes iguales.
- Los percentiles son 99: P1, P2 ... , P99, que delimitan al 1%, al 2%, ... , 99% de los datos, respectivamente.
- P50 coincide con la mediana.
Cálculo de los percentiles
Para calcular los percentiles es necesario que los N datos estén ordenados de menor a mayor.
Procederemos como antes, pero buscaremos el lugar que ocupa cada percentil mediante la expresión
|
|
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
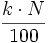 se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el percentil.
se redondea al siguiente número entero, y el dato que ocupe dicho lugar será el percentil.
- Para el caso de datos agrupados en intervalos, la fórmula queda como sigue:
- Para el caso de datos no agrupados o agrupados puntualmente, el valor
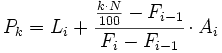
- donde:
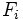 es la frecuencia acumulada del intervalo donde se encuentra el percentil y
es la frecuencia acumulada del intervalo donde se encuentra el percentil y 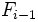 la frecuencia acumulada del intervalo anterior. Se cumple que
la frecuencia acumulada del intervalo anterior. Se cumple que 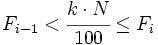 .
.
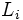 es el límite inferior del intervalo donde se halla el percentil.
es el límite inferior del intervalo donde se halla el percentil.
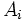 es la amplitud del intervalo donde se halla el percentil.
es la amplitud del intervalo donde se halla el percentil.
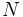 es el número de datos.
es el número de datos.
Percentiles. Ejemplos.
Ejercicios resueltos sobre percentiles.
En esta página web de "Portal Educativo" podrás encontrar ejemplos de cómo se calculan los parámetros de posición.
Cálculo de los cuartiles de una distribución con datos no agrupados.
Cálculo de los cuartiles de una distribución con datos no agrupados.
Cálculo de los deciles de una distribución con datos no agrupados.
Cálculo de los cuartiles de una distribución con datos agrupados puntualmente.
Cálculo de los cuartiles, deciles y percentiles de una distribución con datos agrupados en intervalos.
Cálculo de los cuartiles, deciles y percentiles de una distribución con datos agrupados en intervalos.
Cálculo de los cuartiles y del recorrido intercuartílico de una distribución con datos agrupados en intervalos.
Diagrama de caja y bigotes
En esta página web de "Estadística para todos" podrás encontrar ejemplos de diagramas de cajas y bigotes. Podrás aprender a construirlos y a utilizarlos para comparar distintas distribuciones. Ejemplos de construcción de diagramas de cajas y bigotes. |