Plantilla:Definición: Dominio e imagen
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:19 12 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 3: | Línea 3: | ||
| *El conjunto de valores que toma la variable independiente, <math>y\;</math>, se llama '''imagen''', '''recorrido''' o '''rango''' de la función. Se denota <math>Im_f\;</math>. | *El conjunto de valores que toma la variable independiente, <math>y\;</math>, se llama '''imagen''', '''recorrido''' o '''rango''' de la función. Se denota <math>Im_f\;</math>. | ||
| + | *Si un punto (x,y) pertenece a la gráfica de la función entonces se dice que y es la '''imagen''' de x y también que x es la '''antiimagen''' de y. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 13: | Línea 14: | ||
| *'''Dominio:''' El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos: <math>Dom_f=[0,100]\;</math> | *'''Dominio:''' El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos: <math>Dom_f=[0,100]\;</math> | ||
| *'''Recorrido:''' El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros: <math>Im_f=[0,200]\;</math> | *'''Recorrido:''' El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros: <math>Im_f=[0,200]\;</math> | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Dominio e imagen de una función | ||
| - | |descripcion=Actividades en las que aprenderás de forma visual los conceptos de dominio y recorrido de una función. | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena9/3quincena9_contenidos_2a.htm | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Videotutoriales|titulo=Dominio e imagen de una función|enunciado= | ||
| - | {{Video_enlace_abel | ||
| - | |titulo1=Tutorial 1 | ||
| - | |duracion=13´00" | ||
| - | |url1=https://www.youtube.com/watch?v=bqlbWVFZwE8 | ||
| - | |sinopsis=Conceptos de dominio y rango de una función. Ejemplos | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_clasematicas | ||
| - | |titulo1=Tutorial 2 | ||
| - | |duracion=10'16" | ||
| - | |url1=https://www.youtube.com/watch?v=iKEPhG0xiTY&index=6&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3 | ||
| - | |sinopsis=Tutorial en el que se explica el cálculo del dominio y la imagen de una función dada su gráfica. | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{geogebra: dominio e imagen de una funcion}} | ||
| - | {{p}} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Imagen y antiimagen | ||
| - | |descripcion=Actividades con las que aprenderás los conceptos de imagen y antiimagen. | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena9/3quincena9_contenidos_1c.htm | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
- El conjunto de valores de la variable independiente,
, para los que hay un valor de la variable dependiente, 
, se llama dominio de definición de la función. Se denota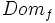 
.
- El conjunto de valores que toma la variable independiente, , se llama imagen, recorrido o rango de la función. Se denota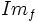
.
- Si un punto (x,y) pertenece a la gráfica de la función entonces se dice que y es la imagen de x y también que x es la antiimagen de y.
"Un grifo vierte agua en un depósito de 200 litros de capacidad, a razón de 2 litros por segundo, hasta que se llena el depósito, momento en el cual se cierra el grifo."
- t = "Tiempo que está abierto el grifo".
- V = "Volumen de agua que se ha llenado el depósito".
- Dominio: El tiempo que el grifo puede estar abierto es un número que varía entre 0 segundos y 100 segundos:
![Dom_f=[0,100]\;](/wikipedia/images/math/a/b/d/abd624243bc89fe5a2233724f02b4f4a.png)
- Recorrido: El volumen de agua que se ha llenado el depósito es un número que varía ente 0 litros y 200 litros:
![Im_f=[0,200]\;](/wikipedia/images/math/3/9/f/39fa0225481adedcbe46a7b134738d1a.png)
