Interés compuesto

De Wikipedia

(Diferencia entre revisiones)

-{{Menú Matemáticas 3ESO
+{{Menú Matemáticas Contenidos Generales
 |ir=
 |ampliar=
 }}
 {{p}}
-{{Teorema
+{{Interes compuesto}}
-|titulo=Fórmula del interés compuesto
-|enunciado=
-El capital final <math>C_F\;\!</math> obtenido a partir de un capital inicial <math>C \;\!</math> a un interés o rédito <math>r\;\!</math>, durante un tiempo <math>n\;\!</math> es:
-{{Caja|contenido=<math>C_F=C \cdot \left (1+\frac{r}{100}\right )^n</math>}}
-'''Nota:''' El rédito <math>r\;\!</math> y el tiempo <math>n\;\!</math> vienen dados en las mismas unidades de tiempo, que pueden ser: años, semestres, trimestres, meses, días, etc.
+[[Categoría: Matemáticas]][[Categoría: Números]]
-|demo=
-Al depositar una cantidad de dinero <math>C \;\!</math> en una entidad bancaria, ésta genera, al cabo del tiempo, unos beneficios llamados '''intereses'''. Supongamos que el tipo de interés o '''rédito''' pactado sea <math>r%\;\!</math> anual, entonces, al ser un problema de encadenamiento de aumento porcentual, cada año que pasa debemos multiplicar el capital inicial <math>C \;\!</math> por el índice de variación <math>\left (1+\frac{r}{100}\right )</math>. Así, el capital final o acumulado en <math>n\;\!</math> años será:
-<center><math>C_F=C \cdot \begin{matrix} \ \\ \underbrace{ \left (1+\frac{r}{100}\right ) \cdot \left (1+\frac{r}{100}\right ) \cdots \left (1+\frac{r}{100}\right ) } \\ n \ veces \end{matrix}= C \cdot \left (1+\frac{r}{100}\right )^n</math></center>
-}}
-{{p}}
-{{Ejemplo|titulo=Ejemplos: ''Interés compuesto''
-|enunciado=
-#¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años?
-#¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años, si el periodo de capitalización es mensual (paga los intereses cada mes)?
-|sol= 1) <math> C_F=10000 \cdot \left (1+\frac{6}{100}\right )^5=10000 \cdot 1,06^5=13382,26</math> €
-) Al ser el 6% anual, el tanto por ciento mensual será <math>\cfrac{6}{12}=0,5%</math> y el número de meses en 5 años es <math>12 \cdot 5 = 60</math> meses.
-Aplicando el encadenamiento de aumento porcentual, tenemos:
-<center><math> C_F=10000 \cdot \left (1+\frac{0,5}{100}\right )^{60}=10000 \cdot 1,005^{60}=13488,50</math> €</center>{{p}}
-Como se puede deducir el periodo de capitalización mensual es mucho más favorable que el anual para el cliente.
-}}
-{{p}}

Revisión actual

Menú: [Mostrar]

Enlaces internos	Para repasar	Enlaces externos
Indice		WIRIS Geogebra Calculadora

Fórmula del interés compuesto

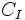El capital final, $C_F\;\!$ , obtenido a partir de un capital inicial, $C_I \;\!$ , a un interés o rédito $r\;\!$ , durante un tiempo $n\;\!$ es:

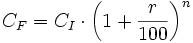
$C_F=C_I \cdot \left (1+\frac{r}{100}\right )^n$

Nota: El rédito $r\;\!$ y el tiempo $n\;\!$ vienen dados en las mismas unidades de tiempo, que pueden ser: años, semestres, trimestres, meses, días, etc., dependiendo del periodo de capitalización que se establezca (pago de intereses anual, mensual, etc.)

Demostración:[Mostrar]

Al depositar una cantidad de dinero 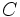$C \;\!$ en una entidad bancaria, ésta genera, al cabo del tiempo, unos beneficios llamados intereses. Supongamos que el tipo de interés o rédito pactado sea 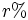$r%\;\!$ anual, entonces, al ser un problema de encadenamiento de aumento porcentual, cada año que pasa debemos multiplicar el capital inicial 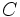$C \;\!$ por el índice de variación 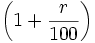$\left (1+\frac{r}{100}\right )$ . Así, el capital final o acumulado en $n\;\!$ años será:

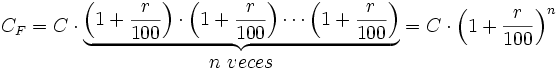
$C_F=C \cdot \begin{matrix} \ \\ \underbrace{ \left (1+\frac{r}{100}\right ) \cdot \left (1+\frac{r}{100}\right ) \cdots \left (1+\frac{r}{100}\right ) } \\ n \ veces \end{matrix}= C \cdot \left (1+\frac{r}{100}\right )^n$

Ejemplos: Interés compuesto

¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años?
¿En cuánto se transforma 10000 € depositados en un banco al 6% anual, al cabo de 5 años, si el periodo de capitalización es mensual (paga los intereses cada mes)?

Solución:[Mostrar]

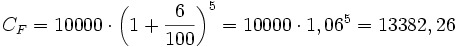1) $C_F=10000 \cdot \left (1+\frac{6}{100}\right )^5=10000 \cdot 1,06^5=13382,26$ €

2) Al ser el 6% anual, el tanto por ciento mensual será 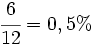$\cfrac{6}{12}=0,5%$ y el número de meses en 5 años es 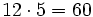$12 \cdot 5 = 60$ meses.

Aplicando el encadenamiento de aumento porcentual, tenemos:

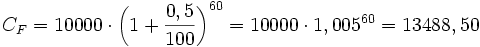$C_F=10000 \cdot \left (1+\frac{0,5}{100}\right )^{60}=10000 \cdot 1,005^{60}=13488,50$ €

Como se puede deducir el periodo de capitalización mensual es mucho más favorable que el anual para el cliente.

Interés compuesto Descripción: [Mostrar]

Actividades en las que aprenderás a manejar la fórmula del interés compuesto.

Interés simple vs. interés compuesto [Mostrar]

Tutorial 1 (4'58") Sinopsis:[Mostrar]

Tutorial que explica el interés simple y el interés compuesto.

Tutorial 2 (24'13") Sinopsis:[Mostrar]

Tutorial que explica los problemas de interés simple e interés compuesto, no como algo diferente si no como casos particulares de problemas de porcentajes y proporciones compuestos.

00:00 a 09:20: Introducción: Ejercicios 1 y 2. Diferencias entre el interés simple y compuesto.
09:20 a 12:48: Ejercicio 3, interés simple.
12:48 a 17:35: Ejercicio 4, interés compuesto.
17:35 a 24:13: Ejercicio 5, interés compuesto (Intereses en cualquier instante).

Obtenido de "http://maralboran.org/wikipedia/index.php/Inter%C3%A9s_compuesto"

Categorías: Matemáticas | Números