Plantilla:Cubo
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 15:55 14 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| + | {{Caja_Amarilla|texto= | ||
| Un caso particular de ortoedro es el '''cubo''' cuyas caras son todas cuadradas. | Un caso particular de ortoedro es el '''cubo''' cuyas caras son todas cuadradas. | ||
| Línea 13: | Línea 14: | ||
| :<math>a\;\!</math>: arista. | :<math>a\;\!</math>: arista. | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás ver el desarrollo de un ortoedro y calcular su volumen y su área. | ||
| - | |enlace=[https://ggbm.at/bEyWk8bY Desarrollo, área y volumen del ortoedro] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_unicoos | + | {{Videos: Area y volumen del cubo}} |
| - | |titulo1=Ejemplo: Área y volumen de un cubo | + | {{AI_enlace |
| - | |duracion=4'59" | + | |descripcion=Actividades de autoevaluación sobre volúmenes de cubos. |
| - | |sinopsis=Cálculo del área y volumen de un cubo | + | |url1=http://www3.gobiernodecanarias.org/medusa/contenidosdigitales/programasflash/cnice/Primaria/Matematicas/Volumen/a3/x5x10.html |
| - | |url1=http://www.unicoos.com/video/matematicas/2-eso/volumen-de-cuerpos-geometricos/cuerpos-de-revolucion/volumen-y-superficie-de-un-cubo | + | |titulo1=Volumen del cubo |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Video_enlace_abel | + | |
| - | |titulo1=Ejercicio | + | |
| - | |duracion=2'31" | + | |
| - | |sinopsis=Cálculo de la diagonal de un cubo a partir de su arista. | + | |
| - | |url1=https://www.youtube.com/watch?v=OyJbwqE3Yh8 | + | |
| - | }} | + | |
| - | {{Video_enlace_matemovil | + | |
| - | |titulo1=Problema | + | |
| - | |duracion=1'57" | + | |
| - | |sinopsis=Halla el volumen de un cubo cuya superficie total es de 36 cm<sup>2</sup>. | + | |
| - | |url1=https://www.youtube.com/watch?v=Id1XfNB_ftY | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Cálculo del área y volumen de un cubo
Halla el volumen de un cubo cuya superficie total es de 36 cm2.
María tiene una caja para guardar juguetes con forma de cubo cuya arista mide 60 cm. ¿Cuántos m2 de plástico se utilizaron para construirla?. ¿Qué volumen tiene en m3?
Actividades de autoevaluación sobre volúmenes de cubos.
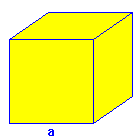
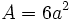
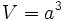
 : arista.
: arista.

