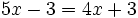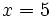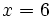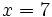Plantilla:Resolver una ecuación 1ºESO
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:24 16 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:02 10 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Resolver una ecuación|enunciado= | ||
| {{Video_enlace_angelmartinez | {{Video_enlace_angelmartinez | ||
| - | |titulo1=Resolver una ecuación | + | |titulo1=Tutorial |
| |duracion=1'00" | |duracion=1'00" | ||
| - | |sinopsis= Ecuaciones. Grado. Soluciones. Ejemplo. | + | |sinopsis=Ecuaciones. Grado. Soluciones. Ejemplo. |
| |url1=https://www.youtube.com/watch?v=ykcrEett-zU | |url1=https://www.youtube.com/watch?v=ykcrEett-zU | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=3'31" | ||
| + | |sinopsis=Comprueba cuál de los siguientes valores es solución de la ecuación <math>5x-3=4x+3\;</math> | ||
| + | |||
| + | :a) <math>x=5\;</math> | ||
| + | :b) <math>x=6\;</math> | ||
| + | :c) <math>x=7\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=eWsC9iES9bE | ||
| + | }} | ||
| }} | }} | ||
| {{AI_anaya|titulo1=Autoevaluación: ''Resolución de ecuaciones'' | {{AI_anaya|titulo1=Autoevaluación: ''Resolución de ecuaciones'' | ||
Revisión de 11:02 10 dic 2017
Resolver una ecuación es hallar su solución o soluciones, si es que existe alguna.
Ejemplo 1:
Para resolver la ecuación 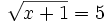 razonaremos de la siguiente manera:
razonaremos de la siguiente manera:
- Como la raíz vale 5, el radicando debe valer 25.
- Si el radicando debe valer 25, entonces x debe ser una unidad menos, x=24.
Esta no es la forma habitual de resolver ecuaciones. Estudiaremos métodos concretos a lo largo del tema.
Ejemplo 2:
La ecuación 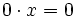 tiene infinitas soluciones, como podrás razonar fácilmente.
tiene infinitas soluciones, como podrás razonar fácilmente.
Ejemplo 3:
- La ecuación
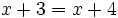 no tiene solución, como podrás razonar fácilmente.
no tiene solución, como podrás razonar fácilmente.
- Lo mismo le ocurre a las ecuaciones del tipo
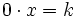 con
con 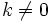 . Por ejemplo,
. Por ejemplo, 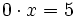 no tiene solución, pues cualquier número multiplicado por 0 nunca puede dar 5.
no tiene solución, pues cualquier número multiplicado por 0 nunca puede dar 5.