Plantilla:Razones trigonométricas de un ángulo cualquiera
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:24 17 dic 2017 Coordinador (Discusión | contribuciones) (→Signo de las razones trigonométricas) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 11: | Línea 11: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Razones trigonométricas de un ángulo de cualquier cuadrante|enunciado= | + | {{Videotutoriales|titulo=Razones trigonométricas de un ángulo cualquiera (usando el círculo unidad)|enunciado= |
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Tutorial | + | |titulo1=Tutorial 1 |
| |duracion=9´51" | |duracion=9´51" | ||
| |url1=https://www.youtube.com/watch?v=98EArSjJw78 | |url1=https://www.youtube.com/watch?v=98EArSjJw78 | ||
| Línea 39: | Línea 39: | ||
| {{p}} | {{p}} | ||
| ===Signo de las razones trigonométricas=== | ===Signo de las razones trigonométricas=== | ||
| - | {{Teorema_sin_demo|titulo=Determinación del signo de las razones trigonométricas|enunciado= | + | El signo de una razón trigonométrica viene determinado por el cuadrante en el que se encuentre el ángulo. |
| - | *'''Signo del coseno:''' Según en qué cuadrante esté el ángulo, el segmento '''OC''' que determina al coseno, puede estar situado a la derecha o a la izquierda del origen '''O'''. Así, el signo del coseno será positivo si está a la derecha de '''O''' y negativo si está a la izquierda. | + | {{p}} |
| - | *'''Signo del seno:''' Según el cuadrante en el que esté el ángulo, el segmento '''CB''' que determina al seno, puede estar situado por encima o por debajo del eje X . Así el signo del seno será positivo si está por encima y negativo si está por debajo. | + | {{Teorema|titulo=Signo de las razones trigonométricas|enunciado= |
| + | *'''Seno:''' El seno de un ángulo es positivo si el ángulo está en el primer o segundo cuadrante, y es negativo si está en el tercer o cuarto cuadrante. | ||
| + | *'''Coseno:''' El coseno de un ángulo es positivo si el ángulo está en el primer o cuarto cuadrante, y es negativo si está en el segundo o tercer cuadrante. | ||
| + | |demo= | ||
| + | *'''Seno:''' Según el cuadrante en el que esté el ángulo, el segmento '''CB''' que determina al seno, puede estar situado por encima o por debajo del eje X . Así el signo del seno será positivo si está por encima (primer y segundo cuadrante) y negativo si está por debajo (tercer y cuarto cuadrante). | ||
| + | |||
| + | *'''Coseno:''' Según en qué cuadrante esté el ángulo, el segmento '''OC''' que determina al coseno, puede estar situado a la derecha o a la izquierda del origen '''O'''. Así, el signo del coseno será positivo si está a la derecha de '''O''' (primer y cuarto cuadrante) y negativo si está a la izquierda (segundo y tercer cuadrante). | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Nota|titulo=Observación:|texto=El signo de las demás razones trigonométricas se deduce fácilmente a partir de los signos del seno y del coseno: | ||
| + | |||
| + | *El signo de la tangente queda determinado a partir del signo del seno y del coseno mediante la regla de los signos. | ||
| + | *El signo de las razones trigonométricas inversas (cosecante, secante y cotangente) son los mismos que los de sus respectivas razones directas (seno, coseno y tangente). | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante. | |descripcion=En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante. | ||
| - | |enlace=[http://ggbm.at/QT4AaGjP Signo de razones trigonométricas de un ángulo cualquiera] | + | |enlace=[http://ggbm.at/QT4AaGjP Signo de las razones trigonométricas de un ángulo cualquiera] |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 55: | Línea 67: | ||
| {{Tabla50|celda1=<center>'''Cuadrante III <br>( seno - / cos - )''' <br> [[Imagen:goniometrica3.png|280px]]</center>|celda2=<center>'''Cuadrante IV <br>( seno - / cos + )''' <br> [[Imagen:goniometrica4.png|280px]]</center>}} | {{Tabla50|celda1=<center>'''Cuadrante III <br>( seno - / cos - )''' <br> [[Imagen:goniometrica3.png|280px]]</center>|celda2=<center>'''Cuadrante IV <br>( seno - / cos + )''' <br> [[Imagen:goniometrica4.png|280px]]</center>}} | ||
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Razones trigonométricas de un ángulo cualquiera|enunciado= | + | {{Videotutoriales|titulo=Construcción gráfica, signo y crecimiento de las razones trigonométricas de un ángulo cualquiera|enunciado= |
| - | {{Video_enlace_fonemato | + | {{Video_enlace_matemovil |
| - | |titulo1=Razones trigonométricas de ángulos orientados | + | |titulo1=Tutorial 1 |
| - | |duracion=5´52" | + | |duracion=40'20" |
| - | |url1=https://www.youtube.com/watch?v=0QKGTIoQqmA&list=PL8C0D37B1235315C7&index=3 | + | |sinopsis= |
| - | |sinopsis=Si el lado origen de un ángulo orientado es el semieje OX, del cuadrante en que está el lado extremo se dice "cuadrante del ángulo". | + | *La circunferencia goniométrica. |
| - | En este video definimos las razones trigonométricas de un ángulo orientado, y para ello empleamos las coordenadas de un punto cualquiera (a;b) del lado extremo. | + | *Definición de las razones trigonométricas usando la circunferencia goniométrica o círculo unidad. |
| + | *Signo de las razones trigonométricas según el cuadrante con una interesante regla mnemotécnica. | ||
| + | *Ejemplos. | ||
| + | *Construcción gráfica de las razones trigonométricas usando el círculo trigonométrico. | ||
| + | |url1=https://www.youtube.com/watch?v=zaifr9Qqk3s&index=30&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33 | ||
| }} | }} | ||
| + | ---- | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=El seno en la circunferencia goniométrica | + | |titulo1=Tutorial 2a: ''El seno'' |
| |duracion=7´26" | |duracion=7´26" | ||
| |url1=https://www.youtube.com/watch?v=sUcQakSvKFk | |url1=https://www.youtube.com/watch?v=sUcQakSvKFk | ||
| Línea 71: | Línea 88: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=El coseno en la circunferencia goniométrica | + | |titulo1=Tutorial 2b: ''El coseno'' |
| |duracion=7´54" | |duracion=7´54" | ||
| |url1=https://www.youtube.com/watch?v=OPV_mEjYGiU | |url1=https://www.youtube.com/watch?v=OPV_mEjYGiU | ||
| Línea 77: | Línea 94: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=La tangente en la circunferencia goniométrica | + | |titulo1=Tutorial 2c: ''La tangente'' |
| |duracion=7´41" | |duracion=7´41" | ||
| |url1=https://www.youtube.com/watch?v=6iTdq2vNwd0 | |url1=https://www.youtube.com/watch?v=6iTdq2vNwd0 | ||
| |sinopsis=Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | |sinopsis=Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | ||
| - | |||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=La cosecante en la circunferencia goniométrica | + | |titulo1=Tutorial 2c: ''La cosecante'' |
| |duracion=15´21" | |duracion=15´21" | ||
| |url1=https://www.youtube.com/watch?v=VjduOmeRh8o | |url1=https://www.youtube.com/watch?v=VjduOmeRh8o | ||
| Línea 90: | Línea 106: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=La secante en la circunferencia goniométrica | + | |titulo1=Tutorial 2d: ''La secante'' |
| |duracion=13´06" | |duracion=13´06" | ||
| |url1=https://www.youtube.com/watch?v=MAMtOCJvIl8 | |url1=https://www.youtube.com/watch?v=MAMtOCJvIl8 | ||
| Línea 96: | Línea 112: | ||
| }} | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=La cotangente en la circunferencia goniométrica | + | |titulo1=Tutorial 2e: ''La cotangente'' |
| |duracion=13´30" | |duracion=13´30" | ||
| |url1=https://www.youtube.com/watch?v=u0O34kVmqPE | |url1=https://www.youtube.com/watch?v=u0O34kVmqPE | ||
| |sinopsis=Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | |sinopsis=Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes. | ||
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | ---- |
| - | |titulo1= Ejercicios 1 | + | {{Video_enlace_matemovil |
| - | |duracion=5´53" | + | |titulo1=Ejercicio 1 |
| - | |url1=https://www.youtube.com/watch?v=12EYvYLU3PE&list=PL8C0D37B1235315C7&index=4 | + | |duracion=27'42" |
| - | |sinopsis=3 ejercicios sobre razones trigonométricas de ángulos orientados. | + | |sinopsis= |
| + | #Sabiendo que <math>sen\,\alpha=\cfrac{2x-5}{3}</math>, halla el intervalo de definición de la variable <math>x\;</math>. | ||
| + | #Halla el valor de la expresión <math>M=\cfrac{cos\,0^\circ+sen\,90^\circ}{cos\,180^\circ+cos\,270^\circ}</math>. | ||
| + | #Indica si es verdadero o falso: | ||
| + | |||
| + | ::a) <math>sen\,200^\circ > sen\,250^\circ</math> | ||
| + | ::b) <math>cos\,200^\circ > cos\,250^\circ</math> | ||
| + | ::c) <math>tg\,200^\circ > tg\,250^\circ</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=NyJbARReKcs&index=31&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33 | ||
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | {{Video_enlace_matemovil |
| - | |titulo1= Ejercicios 2 | + | |titulo1=Ejercicio 2 |
| - | |duracion=6´51" | + | |duracion=9'13" |
| - | |url1=https://www.youtube.com/watch?v=p9Q8kfxmOcQ&list=PL8C0D37B1235315C7&index=5 | + | |sinopsis= |
| - | |sinopsis=3 ejercicios sobre razones trigonométricas de ángulos orientados. | + | *Halla el área de las figuras sombreadas (ver video). |
| + | *Ejercicios propuestos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=-yfCApmsF9M&index=32&list=PL3KGq8pH1bFTdb47fYhuokXPlQKsEeT33 | ||
| }} | }} | ||
| + | |||
| }} | }} | ||
Revisión actual
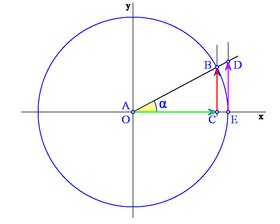
Obsérvese como, en el apartado anterior, las coordenadas del punto B son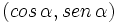 
. Así podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
- Dado un ángulo
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte, B, del lado terminal del ángulo con la circunferencia goniométrica:
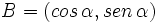
- Definiremos la tangente del ángulo, como:
, 
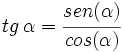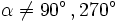
Tutorial 1 (9´51") Sinopsis: - Definición de circunferencia goniométrica o círculo unitario.
- Definición del seno, coseno y tangente de un ángulo a partir de la circunferencia goniométrica.
Ejercicio (12´36") Sinopsis: Asocia las expresiones equivalentes que aparecen en el video.
En esta escena podrás ver como se representan las razones trigonométricas de un ángulo de cualquier cuadrante.
Autoevaluación sobre trigonometría en el círculo unitario.
[editar]
Signo de las razones trigonométricas
El signo de una razón trigonométrica viene determinado por el cuadrante en el que se encuentre el ángulo.
Signo de las razones trigonométricas
- Seno: El seno de un ángulo es positivo si el ángulo está en el primer o segundo cuadrante, y es negativo si está en el tercer o cuarto cuadrante.
- Coseno: El coseno de un ángulo es positivo si el ángulo está en el primer o cuarto cuadrante, y es negativo si está en el segundo o tercer cuadrante.
Demostración:
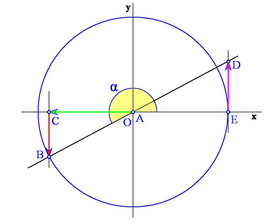
- Seno: Según el cuadrante en el que esté el ángulo, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Así el signo del seno será positivo si está por encima (primer y segundo cuadrante) y negativo si está por debajo (tercer y cuarto cuadrante).
- Coseno: Según en qué cuadrante esté el ángulo, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, el signo del coseno será positivo si está a la derecha de O (primer y cuarto cuadrante) y negativo si está a la izquierda (segundo y tercer cuadrante).
El signo de las demás razones trigonométricas se deduce fácilmente a partir de los signos del seno y del coseno:
- El signo de la tangente queda determinado a partir del signo del seno y del coseno mediante la regla de los signos.
- El signo de las razones trigonométricas inversas (cosecante, secante y cotangente) son los mismos que los de sus respectivas razones directas (seno, coseno y tangente).
En esta escena podrás ver los valores y el signo de las 6 razones trigonométricas de un ángulo de cualquier cuadrante.
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
Cuadrante I
( seno + / cos + )  | Cuadrante II
( seno + / cos - )  |
Cuadrante III
( seno - / cos - )  | Cuadrante IV
( seno - / cos + )  |
Tutorial 1 (40'20") Sinopsis: - La circunferencia goniométrica.
- Definición de las razones trigonométricas usando la circunferencia goniométrica o círculo unidad.
- Signo de las razones trigonométricas según el cuadrante con una interesante regla mnemotécnica.
- Ejemplos.
- Construcción gráfica de las razones trigonométricas usando el círculo trigonométrico.
Tutorial 2a: El seno (7´26") Sinopsis:Interpretación geométrica del seno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Tutorial 2b: El coseno (7´54") Sinopsis:Interpretación geométrica del coseno usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Tutorial 2c: La tangente (7´41") Sinopsis:Interpretación geométrica de la tangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Tutorial 2c: La cosecante (15´21") Sinopsis:Interpretación geométrica de la cosecante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Tutorial 2d: La secante (13´06") Sinopsis:Interpretación geométrica de la secante usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Tutorial 2e: La cotangente (13´30") Sinopsis:Interpretación geométrica de la cotangente usando la circunferencia goniométrica y análisis de su signo y crecimiento según los cuadrantes.
Ejercicio 1 (27'42") Sinopsis: - Sabiendo que
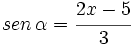, halla el intervalo de definición de la variable 
.
- Halla el valor de la expresión
.
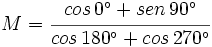- Indica si es verdadero o falso:
- a)
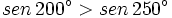
- b)
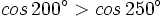
- c)
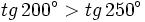
- a)
Ejercicio 2 (9'13") Sinopsis: - Halla el área de las figuras sombreadas (ver video).
- Ejercicios propuestos.
