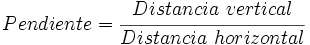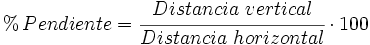Plantilla:Concepto de pendiente

De Wikipedia

Revisión de 19:59 9 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior		Revisión actual Coordinador (Discusión | contribuciones)
Línea 1:		Línea 1:
-	{{Tabla75|celda2=[[Imagen=rampa.png|center]]|celda1={{Caja_Amarilla|texto=En topografía, la '''pendiente''' es la relación que existe entre el desnivel, o distancia en vertical, que debemos superar y la distancia en horizontal que debemos recorrer:	+	{{Tabla75|celda2=[[Imagen:rampa.png|center|250px]]|celda1={{Caja_Amarilla|texto=En topografía, la '''pendiente''' es la relación que existe entre el desnivel, o distancia en vertical, que debemos superar y la distancia en horizontal que debemos recorrer:
	{{caja|contenido=<math>Pendiente = \cfrac{Distancia \ vertical} {Distancia \ horizontal}</math>}}		{{caja|contenido=<math>Pendiente = \cfrac{Distancia \ vertical} {Distancia \ horizontal}</math>}}
	{{p}}		{{p}}
		+	<br>
	Se suele dar en tanto por ciento, para lo cual se multiplica la fracción anterior por 100:		Se suele dar en tanto por ciento, para lo cual se multiplica la fracción anterior por 100:
	{{p}}		{{p}}
-	<center><math>% \, Pendiente = \cfrac{Distancia \ vertical} {Distancia \ horizontal} \cdot 100</math></center>}}	+
		+	{{caja|contenido=<center><math>% \, Pendiente = \cfrac{Distancia \ vertical} {Distancia \ horizontal} \cdot 100</math></center>}}
		+	{{p}}
		+	}}
	}}		}}
	{{p}}		{{p}}
-	Así, por ejemplo, una rampa con un ángulo de inclinación de 45º tiene una pendiente del 100%.	+	{{Ejemplo_simple|titulo=Ejemplo:|contenido=Una rampa con un ángulo de inclinación de 45º tiene una pendiente del 100%, ya que el triángulo formado por la rampa es isósceles.
		+	}}
	{{p}}		{{p}}
-	Este concepto topográfico de pendiente tiene mucho que ver con el concepto de pendiente de una función lineal si consideramos la recta, su gráfica, como si fuese una rampa. No obstante, la pendiente de una función lineal puede tomar valores negativos, mientras que la pendiente topográfica siempre es positiva. Comprueba ésto en la siguiente actividad interactiva.	+	Este concepto topográfico de pendiente tiene mucho que ver con el concepto de pendiente de una función lineal si consideramos la recta, su gráfica, como si fuese una rampa. No obstante, la pendiente de una función lineal puede tomar valores negativos, mientras que la pendiente topográfica siempre es positiva, como podrás comprobar en la siguiente actividad interactiva.
	{{p}}		{{p}}
		+	{{Actividades|titulo=Pendiente|enunciado=
	{{Geogebra_enlace		{{Geogebra_enlace
-	|descripcion=Escena en la que podrás calcular la pendiente de una rampa.	+	|descripcion=Concepto de pendiente. En la escena podrás calcular la pendiente de una rampa.
-	|enlace=[https://ggbm.at/wmGn9JAW Concepto de pendiente]	+	|enlace=[http://ggbm.at/wmGn9JAW Actividad 1]
	}}		}}
-	{{p}}
	{{Geogebra_enlace		{{Geogebra_enlace
	|descripcion=Escena en la que podrás practicar el cálculo de la pendiente a partir de una gráfica.		|descripcion=Escena en la que podrás practicar el cálculo de la pendiente a partir de una gráfica.
-	|enlace=[https://ggbm.at/rqNAmZMB Autoevaluación: Pendiente a partir de la gráfica]	+	|enlace=[http://ggbm.at/rqNAmZMB Autoevaluación 1]
	}}		}}
-	{{p}}
	{{Geogebra_enlace		{{Geogebra_enlace
	|descripcion=Escena en la que podrás practicar dibujando una gráfica que tenga una pendiente dada.		|descripcion=Escena en la que podrás practicar dibujando una gráfica que tenga una pendiente dada.
-	|enlace=[https://ggbm.at/uzZjPrc8 Autoevaluación: Gráfica a partir de la pendiente]	+	|enlace=[http://ggbm.at/uzZjPrc8 Autoevaluación 2]
		+	}}
	}}		}}

---

Revisión actual

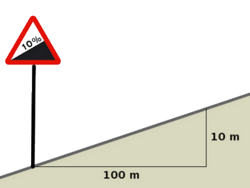
En topografía, la pendiente es la relación que existe entre el desnivel, o distancia en vertical, que debemos superar y la distancia en horizontal que debemos recorrer: Se suele dar en tanto por ciento, para lo cual se multiplica la fracción anterior por 100:

Este concepto topográfico de pendiente tiene mucho que ver con el concepto de pendiente de una función lineal si consideramos la recta, su gráfica, como si fuese una rampa. No obstante, la pendiente de una función lineal puede tomar valores negativos, mientras que la pendiente topográfica siempre es positiva, como podrás comprobar en la siguiente actividad interactiva.