Plantilla:Cálculo de la pendiente

(Diferencia entre revisiones)

Revisión de 13:01 24 dic 2017

Proposición

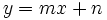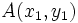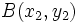Consideremos una función lineal $y=mx+n\;$ y dos puntos $A(x_1,y_1)\;$ y $B(x_2,y_2)\;$ de la recta que la representa.

La pendiente se puede calcular de la siguiente manera:

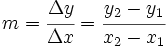
$m=\cfrac {\Delta y}{\Delta x}=\cfrac {y_2-y_1}{x_2-x_1}$

Demostración:

Como 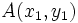$A(x_1,y_1)\;$ es un punto de la recta, verifica su ecuación: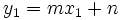 $y_1=mx_1+n\;$

Como 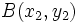$B(x_2,y_2)\;$ es otro punto de la recta, también verifica su ecuación: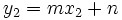 $y_2=mx_2+n\;$

Restando ambas expresiones:

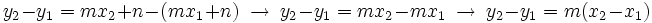
$y_2-y_1=mx_2+n-(mx_1+n) \ \rightarrow \ y_2-y_1=mx_2-mx_1 \ \rightarrow \ y_2-y_1=m(x_2-x_1)$

y despejando m:

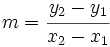
$m=\cfrac{y_2-y_1}{x_2-x_1}$

Cálculo de la pendiente de una recta

Tutorial 1 (16'07") Sinopsis:

En este vídeo se explica como se calcula la pendiente de una recta.
También se resolverá el siguiente problema: Los vértices de un triángulo son los puntos (2,-2), (-1,4) y (4,5). Halla la pendiente de cada uno de sus lados.

Tutorial 2 (7'34") Sinopsis:

Introducción a la pendiente de una recta.

Ejercicio (7'13") Sinopsis:

Encuentra la pendiente de la recta que pasa por los puntos (4,2) y (-3, 16).

Cálculo de la pendiente de una recta

Actividad 1 Descripción:

Escena en la que aprenderás a calcular la pendiente de una función lineal.

Actividad 2 Descripción:

Practica el cálculo de la pendiente de una función lineal a partir de dos puntos.

Autoevaluación Descripción:

La pendiente a partir de dos puntos.

 }}
 {{Video_enlace_khan
-|titulo1=Tutorial 2a
+|titulo1=Tutorial 2
 |duracion=7'34"
 |sinopsis=Introducción a la pendiente de una recta.
 |url1=https://youtu.be/jpIOnLHIxrg
-}}
-{{Video_enlace_khan
-|titulo1=Tutorial 2b
-|duracion=13'43"
-|sinopsis=Ejemplos de cálculo de la pendiente de una recta a partir de su gráfica.
-|url1=https://youtu.be/VA31OVw-6BQ
 }}
 ----