Plantilla:La pendiente y el crecimiento
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:51 7 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=La pendiente <math>m\,</math> de una recta mide la inclinación de la misma, de manera que: | + | {{Teorema_sin_demo|titulo=Propiedades|enunciado=La pendiente, <math>m\,</math>, describe el crecimiento de la función <math>y=mx\,</math>: |
| + | |||
| *Si {{sube|porcentaje=20%|contenido=<math>m>0\,</math>}}, la función es creciente. | *Si {{sube|porcentaje=20%|contenido=<math>m>0\,</math>}}, la función es creciente. | ||
| *Si {{sube|porcentaje=20%|contenido=<math>m<0\,</math>}} la función es decreciente. | *Si {{sube|porcentaje=20%|contenido=<math>m<0\,</math>}} la función es decreciente. | ||
| *Si {{sube|porcentaje=20%|contenido=<math>m=0\,</math>}} la función es constante (recta horizontal). | *Si {{sube|porcentaje=20%|contenido=<math>m=0\,</math>}} la función es constante (recta horizontal). | ||
| + | |||
| + | Además, cuanto mayor es su pendiente (en valor absoluto), más inclinada es su gráfica. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás ver como afecta el signo de la pendiente a su crecimiento. | + | |descripcion=En esta escena podrás ver como afecta el signo de la pendiente al crecimiento de la función. |
| - | |enlace=[https://ggbm.at/nPK8g3jj La pendiente y el crecimiento] | + | |enlace=[http://ggbm.at/nPK8g3jj La pendiente y el crecimiento] |
| }} | }} | ||
Revisión actual
Propiedades
La pendiente, 
, describe el crecimiento de la función 
:
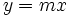- Si
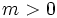, la función es creciente.
- Si
la función es decreciente.
- Si
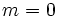la función es constante (recta horizontal).
Además, cuanto mayor es su pendiente (en valor absoluto), más inclinada es su gráfica.
La pendiente y el crecimiento Descripción: En esta escena podrás ver como afecta el signo de la pendiente al crecimiento de la función.
