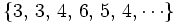Plantilla:Sucesión de números reales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 23:10 13 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una función <math>f \;</math>, que a cada número natural <math>n \;</math> le asocia un número real <math>a_n \;</math> | + | {{Caja_Amarilla|texto=Una '''sucesión''' de números reales es una [[Correspondencia#Tipos de correspondencias. Aplicaciones|función]], <math>f \;</math>, que a cada número natural, <math>n \;</math>, le asocia un único número real, <math>a_n \;</math> |
| <center><math>\begin{matrix}f: & \mathbb{N} & \longrightarrow & \mathbb{R} \\ \ & n & \longrightarrow & a_n \end{matrix}</math></center> | <center><math>\begin{matrix}f: & \mathbb{N} & \longrightarrow & \mathbb{R} \\ \ & n & \longrightarrow & a_n \end{matrix}</math></center> | ||
| Línea 5: | Línea 5: | ||
| Esto genera el conjunto ordenado | Esto genera el conjunto ordenado | ||
| - | <center><math>\{ a_1,\ a_2,\ a_3,\ \cdots \}</math></center> | + | <center><math>\{ a_n \} = \{ a_1,\ a_2,\ a_3,\ \cdots \ \}</math></center> |
| - | que se llaman los '''términos''' de la sucesión. | + | de los '''términos''' de la sucesión. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos <math>\{ a_1,\ a_2,\ a_3,\ \cdots \}</math> en lugar de la sucesión <math>f \;</math>. | + | {{Nota|titulo=Observación:|texto=Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos <math>\{ a_1,\ a_2,\ a_3,\ \cdots \ \}</math> en lugar de la sucesión <math>f \;</math>.}} |
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| Los términos de una sucesión pueden seguir un cierto criterio: | Los términos de una sucesión pueden seguir un cierto criterio: | ||
| + | *<math>\{ 1, \, 3, \, 5, \, 7, \, 9, \, 11, \cdots \}</math>. Sus términos son los números impares. | ||
| - | *<math>\{ 2, 5, 8, 11, 14, 17, \cdots \}</math>. Sus términos se obtienen sumando 3 al anterior. | + | *<math>\{ 2, \, 5, \, 8, \, 11, \, 14, \, 17, \cdots \}</math>. Sus términos se obtienen sumando 3 al anterior. |
| - | *<math>\{ 1, 2, 4, 8, 16, 32, \cdots \}</math>. Sus términos son las potencias de 2. | + | *<math>\{ 1, \, 2, \, 4, \, 8, \, 16, \, 32, \cdots \}</math>. Sus términos son las potencias de 2. |
| - | *<math>\{ 1, -1, 2, -2, 3, -3, \cdots \}</math>. Sus términos van ascendiendo y alternando el signo. | + | *<math>\{ 1, \, -1, \, 2, \, -2, \, 3, \, -3, \cdots \}</math>. Sus términos van ascendiendo y alternando el signo. |
| - | *<math>\{ 2, 3, 5, 8, 13, 21, \cdots \}</math>. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores. | + | *<math>\{ 2, \, 3, \, 5, \, 8, \, 13, \, 21, \cdots \}</math>. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores. |
| o no seguir ninguno: | o no seguir ninguno: | ||
| - | *<math>\{ 3, 1, -2, 77, 5, \cdots \}</math> | + | *<math>\{ 3, \, 3, \, 4, \, 6, \, 5, \, 4, \cdots \}</math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace2 | + | {{Video_enlace_clasematicas |
| - | |titulo1=Función o aplicación entre conjuntos | + | |titulo1=Las sucesiones numéricas |
| - | |duracion=6´25" | + | |duracion=21´07" |
| - | |sinopsis=El concepto de función o aplicación ente dos conjuntos es necesario para la definición de sucesión. | + | |url1=https://www.youtube.com/watch?v=8W0vFci064Y&index=1&list=PLZNmE9BEzVIkITepuGQcKXJ-FuD5p7cP5 |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/01-aplicacion-entre-conjuntos-2#.VCVi6hZ8HA8 | + | |sinopsis=*Tutorial en el que se introducen los conceptos básicos de las sucesiones numéricas. |
| + | *(05:20): Definiciones básicas (sucesión, términos e índices) y ejemplo inicial. | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Sucesión de números reales | ||
| + | |descripcion=Actividades en las que aprenderás a obtener los términos de una sucesión a partir de una regla de formación dada. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena5/3quincena5_contenidos_1a.htm | ||
| }} | }} | ||
Revisión actual
Una sucesión de números reales es una función, 
, que a cada número natural, 
, le asocia un único número real, 
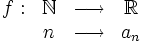
Esto genera el conjunto ordenado
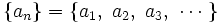
de los términos de la sucesión.
Se suele identificar a la sucesión con sus términos. Normalmente hablaremos de la sucesión de términos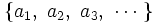 
en lugar de la sucesión .
Los términos de una sucesión pueden seguir un cierto criterio:
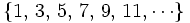. Sus términos son los números impares.
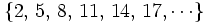. Sus términos se obtienen sumando 3 al anterior.
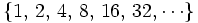. Sus términos son las potencias de 2.
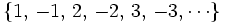. Sus términos van ascendiendo y alternando el signo.
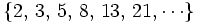. Sus términos, a partir del tercero, se obtienen sumando los dos anteriores.
o no seguir ninguno:
Las sucesiones numéricas (21´07") Sinopsis:- Tutorial en el que se introducen los conceptos básicos de las sucesiones numéricas.
- (05:20): Definiciones básicas (sucesión, términos e índices) y ejemplo inicial.
Sucesión de números reales Descripción: Actividades en las que aprenderás a obtener los términos de una sucesión a partir de una regla de formación dada.
