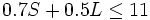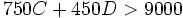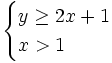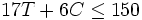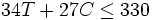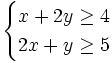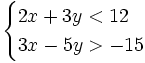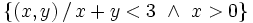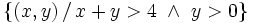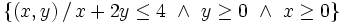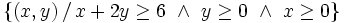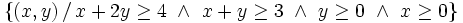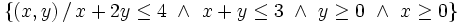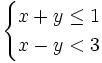Inecuaciones lineales con dos incógnitas (1ºBach)

De Wikipedia

(Diferencia entre revisiones)

Revisión actual

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Geogebra Calculadoras

(pág. 88)

Tabla de contenidos

1 Inecuaciones lineales con dos incógnitas
- 1.1 Resolución de inecuaciones lineales con dos incógnitas
- 1.2 Ejercicios propuestos
2 Sistemas de inecuaciones lineales con dos incógnitas
- 2.1 Resolución de sistemas de inecuaciones lineales con dos incógnitas
- 2.2 Ejercicios propuestos
3 Ejercicios

[editar]

Inecuaciones lineales con dos incógnitas

Una inecuación lineal con dos incógnitas es una inecuación, en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de primer grado con dos variables. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas generales:

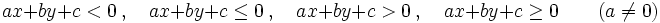
$ax+by+c<0 \ , \quad ax+by+c \le 0 \ , \quad ax+by+c>0 \ , \quad ax+by+c \ge 0 \qquad (a \ne 0)$

donde 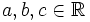$a,b,c \in \mathbb{R}$ son los coeficientes y $x \;$ e $y \;$ son las dos variables.

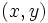Una solución de una inecuación lineal con dos incógnitas, $x\;$ e $y\;$ , es una pareja de valores de las variables, $(x,y)\;$ , que hace que se cumpla la desigualdad.

Inecuaciones lineales con dos incógnitas

Tutorial (6´55") Sinopsis:

Definición de inecuación.
Ejemplos de inecuaciones lineales con dos incógnitas.

Ejercicio 1 (6´07") Sinopsis:

Determina si las parejas (3,5) y (1,-7) son soluciones de la inecuación 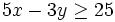$5x-3y \ge 25\;$

Problema 1 (3´08") Sinopsis:

Fabiano quiere lograr al menos 6.5 puntos en un importante torneo de ajedrez. El logra 1 punto por cada partida ganada y 0.5 por cada una empatada. Si llamamos W al número de partidas ganadas y D al número de partidas empatadas, escribe la inecuación que relaciona estas variables con los puntos necesarios para conseguir su objetivo.

Problema 2 (4´45") Sinopsis:

Ezra disfruta de la jardinería. Cada girasol que el riega requiere 0.7 litros de agua y cada azucena requiere 0.5 litros. Ezra tiene un total de 11 litros de agua para estas plantas. En la siguiente desigualdad S representa el número de girasoles y L el número de azucenas que Ezra puede regar:

$0.7S+0.5L \le 11$

Si Ezra riega 10 azucenas, ¿cuántos girasoles podrá regar como máximo con el agua que le sobra?

Problema 3 (5´20") Sinopsis:

Goku quiere tener más de 9000 comentarios en sus videos de YouTube. Él recibe el mismo número de comentarios por cada video de gatos que sube y también el mismo número de comentarios por cada video de perros que sube (aunque el número de comentarios por los videos de perros es distinto que por los de gatos). En la siguiente inecuación, que representa las condiciones para que Goku consiga su meta, C representa el número de videos de gatos y D el de perros:

$750 C+450 D > 9000\;$

Contesta:

a) ¿Cuántos comentarios recibe cada video de gatos? ¿Y cada video de perros?

b) ¿Puede Goku lograr su meta si sube 8 videos de gatos y 7 de perros?

Inecuaciones lineales con dos incógnitas

Autoevaluación 1 Descripción:

Soluciones de inecuaciones lineales con 2 incógnitas.

Autoevaluación 2 Descripción:

Problemas verbales sobre inecuaciones lineales con 2 incógnitas.

[editar]

Resolución de inecuaciones lineales con dos incógnitas

Para resolver estas inecuaciones recurriremos a un método gráfico.

Resolución de las inecuaciones lineales con dos incógnitas

Las soluciones de una inecuación lineal con dos incógnitas dada en forma general (alguna de las dadas en la definición) son los puntos de uno de los dos semiplanos que se encuentran a cada lado de la recta 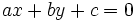$ax+by+c=0 \;$ .

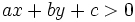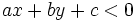Los puntos de uno de los semiplanos cumplen la condición $ax+by+c>0 \;$ y los del otro, la condición $ax+by+c<0 \;$ .

Así, para determinar el semiplano solución, se elige un punto de cualquiera de ellos, y se comprueba si cumple la inecuación. Si la cumple, el semiplano que contiene al punto elegido es la solución, y si no, lo es el otro.

Si la inecuación no es estricta, los puntos de la recta también son solución, ya que para ellos se verifica la igualdad.

Ejercicio resuelto: Inecuaciones lineales con dos incógnitas

1. Resuelve la siguiente inecuación:

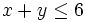
$x+y \le 6\;$

Solución:

Solución 1 Descripción:

En esta escena de Geogebra podrás ver como se representa gráficamente las soluciones de la inecuación 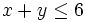$x+y \le 6\;$ .

Resolución de inecuaciones lineales con dos incógnitas

Tutorial 1 (6´13") Sinopsis:

Inecuaciones lineales con dos incógnitas. Ejemplos.

Tutorial 2a (7'30") Sinopsis:

Resolución de inecuaciones lineales con dos incógnitas. Ejemplos.

Tutorial 2b (7'25") Sinopsis:

Resolución de inecuaciones lineales con dos incógnitas. Ejemplos.

Tutorial 2c (14'03") Sinopsis:

Resolución de inecuaciones lineales con dos incógnitas. Ejemplos.

Ejercicio 1 (7´14") Sinopsis:

Resuelve gráficamente la inecuación: 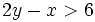$2y-x > 6 \;$

Ejercicio 2 (8´05") Sinopsis:

Resuelve gráficamente las inecuaciones:

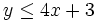
a) $y \le 4x+3 \;$

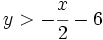
b) $y>-\cfrac{x}{2}- 6 \;$

Ejercicio 3 (3´04") Sinopsis:

Resuelve gráficamente la inecuación: 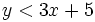$y < 3x+5 \;$

Ejercicio 4 (3´21") Sinopsis:

Encuentra la inecuación que tenga como solución la dada en la gráfica que se muestra en el video.

Problema 1 (7´44") Sinopsis:

Problema de resolución de inecuaciones con dos variables a partir de una gráfica dada.

Resolución de inecuaciones lineales con dos incógnitas

Autoevaluación 1a Descripción:

Soluciones de inecuaciones lineales con 2 incógnitas.

Autoevaluación 1b Descripción:

Resolución de inecuaciones lineales con 2 incógnitas.

Autoevaluación 1c Descripción:

Obtención de inecuaciones lineales con 2 incógnitas a partir de una gráfica.

Autoevaluación 2 Descripción:

Autoevaluación sobre inecuaciones lineales con 2 incógnitas.

[editar]

Ejercicios propuestos

Ejercicios propuestos: Inecuaciones lineales con dos incógnitas

(pág. 88)

1b; 2

Solución:

Nota: Utiliza Geogebra para comprobar las soluciones:

(pág. 89)

[editar]

Sistemas de inecuaciones lineales con dos incógnitas

Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de inecuaciones lineales con una incógnita.
Una solución de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.

Sistemas de inecuaciones lineales

Ejercicio 1 (1´19") Sinopsis:

Determina si el punto (2,5) es solución del sistema

$\begin{cases}y \ge 2x+1 \\ x>1\end{cases}$

Problema 1 (4´58") Sinopsis:

Un pastelito requiere 35 gramos de azúcar y 50 gramos de harina, mientras que un panquecito requiere 30 gramos de azúcar y 65 gramos de harina. Susana necesita usar al menos 460 gramos de azúcar para hacer pastelitos y panquecitos, y no quiere usar más de 970 gramos de harina.

Sea C el número de pastelitos y M el de panquecitos que hace. Escribe un sistema de inecuaciones que represente las condiciones de Susana. Ten e cuenta que la primera inecuación debe representar la condición basada en el número de gramos de azúcar y la segunda debe representar la condición basada en el número de gramos de harina.

Problema 2 (5´21") Sinopsis:

Flor quiere hacer mesas y sillas. Cada mesa está hecha con el mismo número de tablas de madera y clavos. Lo mismo ocurre con cada silla, aunque los número varían con respecto a los de la mesa. Ella tiene un total de 150 tablas y 330 clavos.

Representemos por T a el número de mesas y por C al de sillas.

La siguiente inecuación relaciona el número de tablas de madera utilizado y las tablas disponibles:

$17 T+ 6 C \le 150$

y la siguiente inecuación relaciona el número de clavos utilizado y los clavos disponibles:

$34 T+ 27 C \le 330$

¿Tiene Flor suficientes tablas y clavos para hacer 3 mesas y 9 sillas?

Sistemas de inecuaciones lineales

Autoevaluación 1 Descripción:

Soluciones de sistemas de inecuaciones lineales con 2 incógnitas.

Autoevaluación 2 Descripción:

Problemas sobre soluciones de sistemas de inecuaciones lineales con 2 incógnitas.

[editar]

Resolución de sistemas de inecuaciones lineales con dos incógnitas

Para averiguar las soluciones de un sistema de este tipo recurriremos al método gráfico, igual que se hace con una sola inecuación.

Resolución de las inecuaciones lineales con dos incógnitas

La solución de un sistema de inecuaciones lineales es la intersección de los semiplanos solución de cada una de las inecuaciones que forman el sistema.

Ejercicio resuelto: Sistemas de inecuaciones lineales con dos incógnitas

1. Resuelve el siguiente sistema:

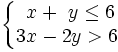
$\left\{\begin{matrix}~x+~y \le 6 \\ 3x-2y > 6 \end{matrix} \right.$

Solución:

Solución 1 Descripción:

En esta escena de Geogebra podrás ver como se representa gráficamente las soluciones del sistema 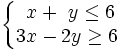$\left\{\begin{matrix}~x+~y \le 6 \\ 3x-2y \ge 6 \end{matrix} \right.$ .

Resolución de sistemas de inecuaciones lineales con 2 incógnitas

Tutorial (5´51") Sinopsis:

Resolución de sistemas de inecuaciones lineales con 2 incógnitas. Ejemplos.

Tutorial 2a (8'46") Sinopsis:

Resolución de sistemas de inecuaciones lineales con 2 incógnitas. Ejemplos.

Tutorial 2b (12'55") Sinopsis:

Resolución de sistemas de inecuaciones lineales con 2 incógnitas. Ejemplos.

Ejercicio 1 (9´30") Sinopsis:

Resuelve gráficamente el siguiente sistema de inecuaciones:

$\begin{cases}x+2y \ge 4 \\ 2x+y \ge 5 \end{cases}$

Ejercicios 2 (12´49") Sinopsis:

Representa gráficamente las siguientes inecuaciones:

$\begin{cases}2x+3y<12 \\3x-5y>-15 \end{cases}$

Ejercicios 3 (12´31") Sinopsis:

Representa gráficamente los siguientes conjuntos:

$\left\{ (x,y) \, / \, x+y<3 \ \and \ x>0 \right\}$
$\left\{ (x,y) \, / \, x+y>4 \ \and \ y>0 \right\}$
$\left\{ (x,y) \, / \, x+2y \le 4 \ \and \ y \ge 0 \ \and \ x \ge 0\right\}$
$\left\{ (x,y) \, / \, x+2y \ge 6 \ \and \ y \ge 0 \ \and \ x \ge 0 \right\}$

Ejercicios 4 (4´59") Sinopsis:

Representa gráficamente los siguientes conjuntos:

$\left\{ (x,y) \, / \, x+2y \ge 4 \ \and \ x+y \ge 3 \ \and \ y \ge 0 \ \and \ x \ge 0 \right\}$
$\left\{ (x,y) \, / \, x+2y \le 4 \ \and \ x+y \le 3 \ \and \ y \ge 0 \ \and \ x \ge 0 \right\}$

Ejercicio 5 (5´40") Sinopsis:

Resuelve gráficamente el siguiente sistema de inecuaciones:

$\begin{cases}y>x-8 \\ y< 5-x \end{cases}$

Ejercicio 6 (3´26") Sinopsis:

Resuelve gráficamente el siguiente sistema de inecuaciones:

$\begin{cases}y>2x+1 \\ y< 2x-5 \\ x>1 \end{cases}$

Ejercicio 7 (6´04") Sinopsis:

Resuelve gráficamente el siguiente sistema de inecuaciones:

$\begin{cases}x+y \le 1 \\ x-y< 3 \end{cases}$

Problema 1 (8´24") Sinopsis:

Luis recibió una tarjeta de regalo por valor de $25 de una tienda online dedicada a la venta de música digital y juegos. Cada canción cuesta $1, y cada juego $2. Si él quiere comprar al menos 15 artículos con su tarjeta de regalo, escribe un sistema de inecuaciones que represente el problema e identifica el rango de posibles compras utilizando una gráfica.

Problema 2 (4´25") Sinopsis:

Resuelve un problema de sistemas de inecuaciones a partir de la gráfica dada en el video.

Resolución de sistemas de inecuaciones lineales con 2 incógnitas

Autoevaluación 1 Descripción:

Resolución de sistemas de inecuaciones lineales con dos incógnitas.

Autoevaluación 2 Descripción:

Autoevaluación sobre sistemas de inecuaciones lineales con dos incógnitas.

[editar]

Ejercicios propuestos

Ejercicios propuestos: Sistemas de inecuaciones lineales con dos incógnitas

(pág. 89)

3b,d,f,g,h

3a,c,e

Solución:

Nota: Utiliza Geogebra para comprobar las soluciones:

[editar]

Ejercicios

Ejercicios 1: Inecuaciones con una o dos incógnitas Descripción:

Ejercicios resueltos sobre inecuaciones con una o dos incógnitas.

Ejercicios 2: Inecuaciones de primer grado con una o dos incógnitas Descripción:

Ejercicios resueltos sobre inecuaciones de primer grado con una o dos incógnitas.

Ejercicios 3: Sistemas de inecuaciones de primer grado con una o dos incógnitas Descripción:

Ejercicios resueltos sobre sistemas de inecuaciones de primer grado con una o dos incógnitas.

Autoevaluación: Comparando expresiones Descripción:

Elige la inecuación que mejor se adecúe a la situación planteada.

Obtenido de "http://maralboran.org/wikipedia/index.php/Inecuaciones_lineales_con_dos_inc%C3%B3gnitas_%281%C2%BABach%29"

Categorías: Matemáticas | Álgebra

 }}
 {{p}}
-==Inecuación lineal con dos incógnitas==
 (pág. 88)
-{{Caja_Amarilla|texto=Una '''inecuación lineal con dos incógnitas''' es una inecuación, en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de primer grado con dos variables. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
-<center><math>ax+by+c<0 \ , \quad ax+by+c \le 0  \ , \quad ax+by+c>0 \ , \quad ax+by+c \ge 0 \qquad (a \ne 0)</math></center>}}
+==Inecuaciones lineales con dos incógnitas==
+{{Inecuación lineal con dos incógnitas}}
-donde <math>a,b,c \in \mathbb{R}</math> son los coeficientes y <math>x \;</math> e <math>y \;</math> son las dos variables.
 {{p}}
-{{Video_enlace_fonemato
+===Resolución de inecuaciones lineales con dos incógnitas===
-|titulo1=Inecuaciones lineales con dos incógnitas
+{{Resolución de una inecuación lineal con dos incógnitas}}
-|duracion=6´55"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/03-ecuaciones-y-sistemas-de-ecuaciones/06-inecuaciones-lineales-con-dos-incognitas#.VCc6O_l_u2E
-|sinopsis=
-*Definición de inecuación.
-*Ejemplos de inecuaciones lineales con dos incógnitas.
-}}
-{{p}}
-===Resolución de una inecuación lineal con dos incógnitas===
-Para resolver estas inecuaciones recurriremos a un método gráfico.
-{{Teorema_sin_demo|titulo=Resolución de las inecuaciones lineales con dos incógnitas|enunciado=Las soluciones de una inecuación lineal con dos incógnitas son los puntos de uno de los dos semiplanos que se encuentran a cada lado de la recta <math>ax+by+c=0 \;</math>.
-Los puntos de uno de los semiplanos cumplen la condición <math>ax+by+c>0 \;</math> y los del otro, la condición <math>ax+by+c<0 \;</math>.
-Así, para determinar el semiplano solución, se elige un punto de cualquiera de ellos, y se comprueba si cumple la inecuación. Si la cumple, el semiplano que contiene al punto elegido es la solución, y si no, lo es el otro.
-Si la inecuación no es estricta, los puntos de la recta también son solución, ya que para ellos se verifica la igualdad.
-}}
-{{p}}
-(pág. 88)
-{{Ejemplo|titulo=Ejercicio resuelto: ''Inecuaciones lineales con dos incógnitas''
-|enunciado='''1.''' Resuelve la siguiente inecuación:
-<center><math>x+y \le 6\;</math></center>
-|sol=
-{{Geogebra_enlace
-|descripcion=En esta escena de Geogebra podrás ver como se representa gráficamente las soluciones de la inecuación <math>x+y \le 6\;</math>.
-|enlace=[https://www.geogebra.org/m/EH3c9c9f Solución 1]
-}}
-}}
 {{p}}
 }}
-==Sistemas de inecuaciones lineales con dos incógnitas==
 (pág. 89)
-{{Caja Amarilla|texto=*Un '''sistema de inecuaciones lineales con dos incógnitas''' es un conjunto de inecuaciones lineales con una incógnita.
+==Sistemas de inecuaciones lineales con dos incógnitas==
-* Una '''solución''' de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.}}
+{{Sistemas de inecuaciones lineales con dos incógnitas}}
 {{p}}
-===Resolución de un sistema de inecuaciones lineales con dos incógnitas===
+===Resolución de sistemas de inecuaciones lineales con dos incógnitas===
-Para averiguar las soluciones de un sistema de este tipo, recurriremos al método gráfico, igual que se hace con una sola inecuación.
+{{Resolución de un sistema de inecuaciones lineales con dos incógnitas}}
-{{Teorema_sin_demo|titulo=Resolución de las inecuaciones lineales con dos incógnitas|enunciado=
-La solución de un sistema de inecuaciones lineales es la intersección de los semiplanos solución de cada una de las inecuaciones que forman el sistema.}}
-{{p}}
-(pág. 89)
-{{Ejemplo|titulo=Ejercicio resuelto: ''Sistemas de inecuaciones lineales con dos incógnitas''
-|enunciado='''1.''' Resuelve el siguiente sistema:
-<center><math>\left\{\begin{matrix}~x+~y \le 6 \\ 3x-2y > 6 \end{matrix} \right.</math></center>
-|sol=
-{{Geogebra_enlace
-|descripcion=En esta escena de Geogebra podrás ver como se representa gráficamente las soluciones del sistema <math>\left\{\begin{matrix}~x+~y \le 6 \\ 3x-2y \ge 6 \end{matrix} \right.</math>.
-|enlace=[https://ggbm.at/N4Mkb4AR Solución 1]
-}}
-}}
-{{p}}
-{{Videotutoriales|titulo=Sistemas de inecuaciones lineales con 2 incógnitas|enunciado=
-{{Video_enlace_abel
-|titulo1=Ejercicio 1
-|duracion=9´30"
-|url1=https://www.youtube.com/watch?v=xrwXdFCV1W0
-|sinopsis=Resuelve gráficamente el siguiente sistema de inecuaciones:
-# <math>x+2y \ge 4 \;</math>
-# <math>2x+y \ge 5 \;</math>
-}}
-{{Video_enlace_fonemato
-|titulo1=Ejercicios 2
-|duracion=12´49"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/03-ecuaciones-y-sistemas-de-ecuaciones/0601-dos-ejercicios-5-2#.VCc6jvl_u2E
-|sinopsis=Representa gráficamente las siguientes inecuaciones:
-# <math>2x+3y<12 \;</math>
-# <math>3x-5y>-15 \;</math>
-}}
-{{Video_enlace_fonemato
-|titulo1=Ejercicios 3
-|duracion=12´31"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/03-ecuaciones-y-sistemas-de-ecuaciones/0602-cuatro-ejercicios#.VCc6wPl_u2E
-|sinopsis=Representa gráficamente los siguientes conjuntos:
-# <math>\left\{ (x,y) \, / \, x+y<3 , \ x>0 \right\}</math>
-# <math>\left\{ (x,y) \, / \, x+y>4 , \ y>0 \right\}</math>
-# <math>\left\{ (x,y) \, / \, x+2y \le 4 , \ y \ge 0 , \ x \ge 0\right\}</math>
-# <math>\left\{ (x,y) \, / \, x+2y \ge 6 , \ y \ge 0 , \ x \ge 0 \right\}</math>
-}}
-{{Video_enlace_fonemato
-|titulo1=Ejercicios 4
-|duracion=4´59"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/03-ecuaciones-y-sistemas-de-ecuaciones/0603-dos-ejercicios-3#.VCc68vl_u2E
-|sinopsis=Representa gráficamente los siguientes conjuntos:
-# <math>\left\{ (x,y) \, / \, x+2y \ge 4 , \ x+y \ge 3  , \ y \ge 0  , \ x \ge 0 \right\}</math>
-# <math>\left\{ (x,y) \, / \, x+2y \le 4 , \ x+y \le 3  , \ y \ge 0  , \ x \ge 0 \right\}</math>
-}}
-}}
 {{p}}
 }}
 }}
+==Ejercicios==
+{{Ejercicios: Inecuaciones lineales con dos incógnitas}}
 [[Categoría: Matemáticas]][[Categoría: Álgebra]]

Inecuaciones lineales con dos incógnitas (1ºBach)

De Wikipedia

Revisión actual

Tabla de contenidos

Inecuaciones lineales con dos incógnitas

Resolución de inecuaciones lineales con dos incógnitas

Ejercicios propuestos

Sistemas de inecuaciones lineales con dos incógnitas

Resolución de sistemas de inecuaciones lineales con dos incógnitas

Ejercicios propuestos

Ejercicios

Vistas

Herramientas personales

Menú

Buscar

Herramientas