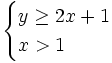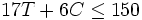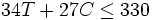Plantilla:Sistemas de inecuaciones lineales con dos incógnitas
De Wikipedia
| Revisión de 18:12 28 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 3: | Línea 3: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Sistemas de inecuaciones lineales|enunciado= | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| - | |titulo1=Sistemas de inecuaciones lineales | + | |titulo1=Ejercicio 1 |
| |duracion=1´19" | |duracion=1´19" | ||
| |url1=https://youtu.be/urgAaz76etc | |url1=https://youtu.be/urgAaz76etc | ||
| Línea 11: | Línea 12: | ||
| :<math>\begin{cases}y \ge 2x+1 \\ x>1\end{cases}</math> | :<math>\begin{cases}y \ge 2x+1 \\ x>1\end{cases}</math> | ||
| }} | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=4´58" | ||
| + | |url1=https://youtu.be/kAdyuk2g_ow | ||
| + | |sinopsis=Un pastelito requiere 35 gramos de azúcar y 50 gramos de harina, mientras que un panquecito requiere 30 gramos de azúcar y 65 gramos de harina. Susana necesita usar al menos 460 gramos de azúcar para hacer pastelitos y panquecitos, y no quiere usar más de 970 gramos de harina. | ||
| + | |||
| + | Sea ''C'' el número de pastelitos y ''M'' el de panquecitos que hace. Escribe un sistema de inecuaciones que represente las condiciones de Susana. Ten e cuenta que la primera inecuación debe representar la condición basada en el número de gramos de azúcar y la segunda debe representar la condición basada en el número de gramos de harina. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=5´21" | ||
| + | |url1=https://youtu.be/sE1NafwpCrg | ||
| + | |sinopsis=Flor quiere hacer mesas y sillas. Cada mesa está hecha con el mismo número de tablas de madera y clavos. Lo mismo ocurre con cada silla, aunque los número varían con respecto a los de la mesa. Ella tiene un total de 150 tablas y 330 clavos. | ||
| + | |||
| + | Representemos por ''T'' a el número de mesas y por ''C'' al de sillas. | ||
| + | |||
| + | La siguiente inecuación relaciona el número de tablas de madera utilizado y las tablas disponibles: | ||
| + | |||
| + | :<math>17 T+ 6 C \le 150</math> | ||
| + | |||
| + | y la siguiente inecuación relaciona el número de clavos utilizado y los clavos disponibles: | ||
| + | |||
| + | :<math>34 T+ 27 C \le 330</math> | ||
| + | |||
| + | ¿Tiene Flor suficientes tablas y clavos para hacer 3 mesas y 9 sillas? | ||
| + | |||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Sistemas de inecuaciones lineales|enunciado= | ||
| {{AI_Khan | {{AI_Khan | ||
| - | |titulo1=Sistemas de inecuaciones lineales | + | |titulo1=Autoevaluación 1 |
| - | |descripcion=Autoevaluación sobre soluciones de sistemas de inecuaciones lineales con 2 incógnitas. | + | |descripcion=Soluciones de sistemas de inecuaciones lineales con 2 incógnitas. |
| |url1=http://es.khanacademy.org/math/algebra/two-variable-linear-inequalities/checking-solutions-of-inequalities/e/checking-solutions-to-systems-of-inequalities | |url1=http://es.khanacademy.org/math/algebra/two-variable-linear-inequalities/checking-solutions-of-inequalities/e/checking-solutions-to-systems-of-inequalities | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | |descripcion=Problemas sobre soluciones de sistemas de inecuaciones lineales con 2 incógnitas. | ||
| + | |url1=http://es.khanacademy.org/math/algebra/two-variable-linear-inequalities/modeling-with-linear-inequalities/e/modeling-systems-of-linear-inequalities | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
- Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de inecuaciones lineales con una incógnita.
- Una solución de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.
Ejercicio 1 (1´19") Sinopsis: Determina si el punto (2,5) es solución del sistema
Problema 1 (4´58") Sinopsis: Un pastelito requiere 35 gramos de azúcar y 50 gramos de harina, mientras que un panquecito requiere 30 gramos de azúcar y 65 gramos de harina. Susana necesita usar al menos 460 gramos de azúcar para hacer pastelitos y panquecitos, y no quiere usar más de 970 gramos de harina.
Sea C el número de pastelitos y M el de panquecitos que hace. Escribe un sistema de inecuaciones que represente las condiciones de Susana. Ten e cuenta que la primera inecuación debe representar la condición basada en el número de gramos de azúcar y la segunda debe representar la condición basada en el número de gramos de harina.
Problema 2 (5´21") Sinopsis: Flor quiere hacer mesas y sillas. Cada mesa está hecha con el mismo número de tablas de madera y clavos. Lo mismo ocurre con cada silla, aunque los número varían con respecto a los de la mesa. Ella tiene un total de 150 tablas y 330 clavos.
Representemos por T a el número de mesas y por C al de sillas.
La siguiente inecuación relaciona el número de tablas de madera utilizado y las tablas disponibles:
y la siguiente inecuación relaciona el número de clavos utilizado y los clavos disponibles:
¿Tiene Flor suficientes tablas y clavos para hacer 3 mesas y 9 sillas?
Autoevaluación 1 Descripción: Soluciones de sistemas de inecuaciones lineales con 2 incógnitas.
Autoevaluación 2 Descripción: Problemas sobre soluciones de sistemas de inecuaciones lineales con 2 incógnitas.
