Plantilla:Valor absoluto de una función (1ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 20:10 11 dic 2016
Coordinador (Discusión | contribuciones)
(→Videos sobre el valor absoluto de una función)
← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)
(→Representación gráfica del valor absoluto de una función)
Línea 1: Línea 1:
==Función valor absoluto== ==Función valor absoluto==
{{Tabla50|celda1= {{Tabla50|celda1=
-{{Caja_Amarilla|texto=La función '''valor absoluto''' es aquella que a cada número <math>x\;</math> le asigna su [[Valor absoluto (1ºBach)|valor absoluto]]. Es decir:+{{Caja_Amarilla|texto=La función '''valor absoluto''' es aquella que a cada número <math>x\;</math> le asigna su [[Números reales (1ºBach)#Valor absoluto de un número real|valor absoluto]]. Es decir:
{{b}} {{b}}
<center><math>|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0 <center><math>|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0
Línea 8: Línea 8:
\end{cases} \end{cases}
</math></center> </math></center>
 +}}
{{p}} {{p}}
 +{{Geogebra_enlace
 +|descripcion=Representación de la función valor absoluto.
 +|enlace=[http://ggbm.at/Jssrej9J Función valor absoluto]
}} }}
|celda2= |celda2=
Línea 23: Línea 27:
</math></center> </math></center>
}} }}
-{{p}}{{p}}+{{p}}
-{{Geogebra_enlace+{{Video_enlace_fonemato
-|descripcion=Representación conjunta de una función cualquiera y su valor absoluto.+
-|enlace=[https://ggbm.at/b6uqNbJp Valor absoluto de una función]+
-}}+
- +
-==Videos sobre el valor absoluto de una función==+
-{{Video_enlace2+
|titulo1=Valor absoluto de una función |titulo1=Valor absoluto de una función
|duracion=7'35" |duracion=7'35"
|sinopsis= |sinopsis=
-Siendo "f" y "u" funciones reales de variable real, escribimos f = |u| si f(x) = |u(x)|.+Siendo "f" y "u" funciones reales de variable real, escribimos <math>f = |u|</math> si <math>f(x) = |u(x)|</math>.
*La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos. *La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos.
Línea 40: Línea 38:
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/30-la-funcion-valor-absoluto-3 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/30-la-funcion-valor-absoluto-3
 +}}
 +{{Geogebra_enlace
 +|descripcion=Representación conjunta de una función cualquiera y su valor absoluto.
 +|enlace=[http://ggbm.at/b6uqNbJp Valor absoluto de una función]
 +}}
 +{{p}}
 +===Representación gráfica del valor absoluto de una función===
 +{{Teorema_sin_demo|titulo=Procedimiento|enunciado=
 +Para representar gráficamente el valor absoluto de una función f:
 +
 +#Representamos la función f.
 +#Hacemos una simetría respecto del eje X de la parte de la gráfica de f que está por debajo de dicho eje.
 +#Borramos esa parte de f que está por debajo del eje X.
 +#La parte de la gráfica de f que está por encima del eje X la dejamos tal cual.
 +#La gráfica resultante es la gráfica del valor absoluto de f.
}} }}
{{p}} {{p}}
-{{ejemplo2+{{Videotutoriales|titulo=Representación gráfica del valor absoluto de una función|enunciado=
-|titulo=Ejemplos: ''Valor absoluto de una función''+{{Video_enlace_fonemato
-|enunciado=+|titulo1=Ejercicio 1
-{{Video_enlace2+
-|titulo1=3 ejemplos+
|duracion=10'04" |duracion=10'04"
-|sinopsis=3 ejemplos de representación gráfica del valor absoluto de una función.+|sinopsis=Representa gráficamente:
 + 
 +:a) <math>y=\left| x-2 \right|</math>
 +:b) <math>y=\left| 9-3x \right|</math>
 +:c) <math>y=\left| x^2-6x+5 \right|</math>
 + 
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3001-tres-ejercicios-3 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3001-tres-ejercicios-3
}} }}
-{{Video_enlace2+{{Video_enlace_fonemato
-|titulo1=2 ejemplos+|titulo1=Ejercicio 2
|duracion=8'36" |duracion=8'36"
-|sinopsis=2 ejemplos de representación gráfica del valor absoluto de una función.+|sinopsis=Representa gráficamente:
 + 
 +:a) <math>y=x+ \left| x-2 \right|</math>
 +:b) <math>y=x^2 - \left| x^2-4 \right|</math>
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3002-dos-ejercicios-3 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3002-dos-ejercicios-3
}} }}
-{{Video_enlace2+{{Video_enlace_fonemato
-|titulo1=1 ejemplo+|titulo1=Ejercicio 3
|duracion=4'27" |duracion=4'27"
-|sinopsis=1 ejemplo de representación gráfica del valor absoluto de una función.+|sinopsis=Representa gráficamente: <math>y=x^2 - \left| 4-x^2 \right|</math>
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3003-ejercicio-6 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3003-ejercicio-6
}} }}
 +{{Video_enlace_unicoos
 +|titulo1=Ejercicio 4
 +|duracion=30'33"
 +|sinopsis=Representa gráficamente:
 +
 +:a) <math>f(x)=x+ | x-2 |</math>
 +:b) <math>g(x)=\left| x^2-4 \right|</math>
 +:c) <math>h(x)=| x | - x</math>
 +:d) <math>i(x)=\cfrac{x^2+1}{|x|}</math>
 +:e) <math>j(x)=\left| 2-\sqrt{1-x} \right|</math>
 +
 +|url1=http://www.unicoos.com/video/matematicas/4-eso/funciones-elementales/funciones-a-trozos/funcion-a-trozos-valor-absoluto
}} }}
 +
 +}}
 +{{AI_Khan
 +|titulo1=Representación gráfica del valor absoluto de una función
 +|descripcion=Autoevaluación.
 +|url1=http://es.khanacademy.org/math/algebra/absolute-value-equations-functions/graphs-of-absolute-value-functions/e/graphs-of-absolute-value-functions
 +}}
 +{{p}}

Revisión actual

[editar]

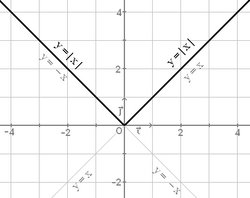
Función valor absoluto

La función valor absoluto es aquella que a cada número 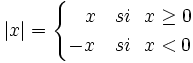x\; le asigna su valor absoluto. Es decir:  

|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0 \\ -x & si \ \ x < 0 \end{cases}

Función valor absoluto     Descripción:

Representación de la función valor absoluto.

[editar]

Valor absoluto de una función

El valor absoluto de una función se define como:  

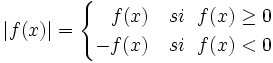
|f(x)|=\begin{cases} \ \ \, f(x) & si \ \ f(x) \ge 0 \\ -f(x) & si \ \ f(x) < 0 \end{cases}

Valor absoluto de una función (7'35")     Sinopsis:

Siendo "f" y "u" funciones reales de variable real, escribimos f = | u | si f(x) = | u(x) | .

  • La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos.
  • En los puntos en que "u" toma valores negativos, la gráfica de "f" es simétrica de la de "u" respecto al eje de abcisas.
Valor absoluto de una función     Descripción:

Representación conjunta de una función cualquiera y su valor absoluto.

[editar]

Representación gráfica del valor absoluto de una función

ejercicio

Procedimiento

Para representar gráficamente el valor absoluto de una función f:

  1. Representamos la función f.
  2. Hacemos una simetría respecto del eje X de la parte de la gráfica de f que está por debajo de dicho eje.
  3. Borramos esa parte de f que está por debajo del eje X.
  4. La parte de la gráfica de f que está por encima del eje X la dejamos tal cual.
  5. La gráfica resultante es la gráfica del valor absoluto de f.

video
Representación gráfica del valor absoluto de una función
Ejercicio 1 (10'04")     Sinopsis:

Representa gráficamente:

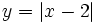
a) y=\left| x-2 \right|
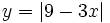
b) y=\left| 9-3x \right|
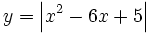
c) y=\left| x^2-6x+5 \right|
Ejercicio 2 (8'36")     Sinopsis:

Representa gráficamente:

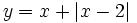
a) y=x+ \left| x-2 \right|
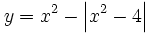
b) y=x^2 - \left| x^2-4 \right|
Ejercicio 3 (4'27")     Sinopsis:

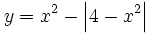
Representa gráficamente: y=x^2 - \left| 4-x^2 \right|

Ejercicio 4 (30'33")     Sinopsis:

Representa gráficamente:

a) f(x) = x + | x − 2 |
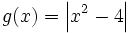
b) g(x)=\left| x^2-4 \right|
c) h(x) = | x | − x
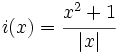
d) i(x)=\cfrac{x^2+1}{|x|}
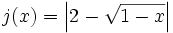
e) j(x)=\left| 2-\sqrt{1-x} \right|

Representación gráfica del valor absoluto de una función     Descripción:

Autoevaluación.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Valor_absoluto_de_una_funci%C3%B3n_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda