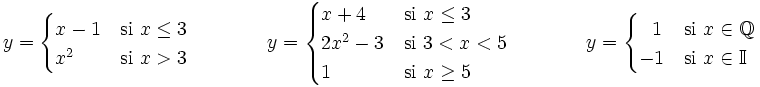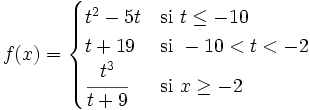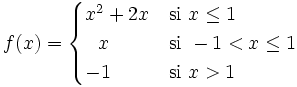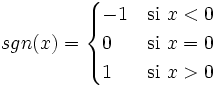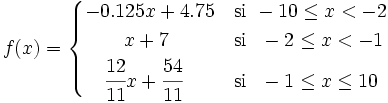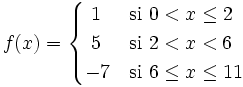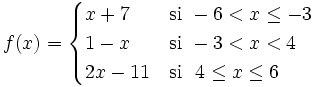Plantilla:Funciones definidas a trozos
De Wikipedia
| Revisión de 08:04 17 abr 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Una '''función definida a trozos''' es aquella que utiliza varias expresiones para su definición, utilizando cada una de ellas en un determinado tramo del dominio de definición de la función principal. | + | Una '''función definida a trozos''' es aquella que utiliza varias funciones para su definición, cada una de ellas definida en un determinado subconjunto del dominio de definición de la función principal. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Desplegable|titulo=Ejemplos:|contenido=Son funciones definidas a trozos: | + | {{Ejemplo_simple|titulo=Ejemplos:|contenido=Son funciones definidas a trozos: |
| :<math>y = \begin{cases} x-1 & \mbox{si }x \le 3 \\ x^2 & \mbox{si }x>3 \end{cases} \qquad \qquad y = \begin{cases} x+4 & \mbox{si }x \le 3 \\ 2x^2-3 & \mbox{si }3<x<5 \\ 1 & \mbox{si }x \ge 5 \end{cases} \qquad \qquad y = \begin{cases} ~~1 & \mbox{si }x \in \mathbb{Q} \\ -1 & \mbox{si }x\in \mathbb{I} \end{cases}</math> | :<math>y = \begin{cases} x-1 & \mbox{si }x \le 3 \\ x^2 & \mbox{si }x>3 \end{cases} \qquad \qquad y = \begin{cases} x+4 & \mbox{si }x \le 3 \\ 2x^2-3 & \mbox{si }3<x<5 \\ 1 & \mbox{si }x \ge 5 \end{cases} \qquad \qquad y = \begin{cases} ~~1 & \mbox{si }x \in \mathbb{Q} \\ -1 & \mbox{si }x\in \mathbb{I} \end{cases}</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Funciones definidas a trozos''|cuerpo= | + | {{Geogebra_enlace |
| - | {{ai_cuerpo | + | |descripcion=En esta escena podrás representar funciones definidas en hasta 4 trozos. |
| - | |enunciado='''Actividad 1:''' Ejemplo de función definida a trozos. | + | |enlace=[http://ggbm.at/JCV99Kf8 Graficador de funciones definidas a trozos] |
| - | |actividad= | + | }} |
| - | En la siguiente escena puedes ver la representación de la función | + | {{p}} |
| + | {{Ejemplo|titulo=Ejemplos: ''Función definida a trozos'' | ||
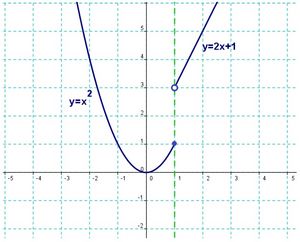
| + | |enunciado=Representa la siguiente función: | ||
| - | <center><math>y = \begin{cases} x+4 & \mbox{si }x \le 3 \\ 7-2(x-3) & \mbox{si }3<x<6 \\ 1 & \mbox{si }x \ge 6 \end{cases}</math></center> | + | <center><math>y = \begin{cases} x^2 & \mbox{si }x \le 1 \\ 2x+1 & \mbox{si }x>1 \end{cases}</math></center> |
| - | Mueve el punto P para ver que expresión corresponde a cada tramo. | + | |sol= |
| + | Para su representación, tenemos que dibujar cada una de las funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición). | ||
| - | <center><iframe> | + | [[Imagen:f_a_trozos_1.jpg|300px|center]] |
| - | url=http://maralboran.org/web_ma/descartes/Analisis/funcion_a_trozos/funcion_a_trozos2_1.html | + | |
| - | width=480 | + | |
| - | height=390 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/descartes/Analisis/funcion_a_trozos/funcion_a_trozos2_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 2:''' El entrenamiento y otros ejemplos de funciones a trozos. | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010939_PRE_0_726754081&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); | + | |
| - | width=100% | + | |
| - | height=600 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010939_PRE_0_726754081&mode=1&rtc=1001&locale=es_ES&cache=false',600,400,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| - | {{ai_cuerpo | + | |
| - | |enunciado='''Actividad 3:''' Une cada función con su gráfica. | + | |
| - | |actividad= | + | |
| - | <center><iframe> | + | |
| - | url=http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010940_AC_0_751125357&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); | + | |
| - | width=100% | + | |
| - | height=600 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://contenidos.santillanaenred.com/jukebox/servlet/GetPlayer?p3v=true&xref=200412010940_AC_0_751125357&mode=1&rtc=1001&locale=es_ES&cache=false',750,540,'snrPop',0); '''Click''' aquí si no se ve bien la escena]</center> | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplo: ''Función definida a trozos'' | + | {{Ejemplo|titulo=Ejemplos: ''Función definida a trozos'' |
| - | |enunciado=Representa la siguiente función: | + | |enunciado=Encuentra la expresión analítica de la función cuya gráfica es la siguiente: |
| + | [[Imagen:funcion_trozos.png|250px|center]] | ||
| + | |sol= | ||
| + | Tendremos que hallar las ecuaciones de tres rectas. Para ello localizaremos dos puntos por los que pase cada recta y a partir de ellos obtendremos su pendiente y luego su ecuación por medio de la ecuación punto-pendiente. | ||
| + | {{p}} | ||
| <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | ||
| - | |sol=Para su representación, tenemos que dibujar cada una de las tres funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición). | ||
| - | <center>[[Imagen:funcion_trozos.png|250px]]</center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad Interactiva: ''Funciones definidas a trozos''|cuerpo= | + | {{Videotutoriales|titulo=Funciones definidas a trozos|enunciado= |
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1a | ||
| + | |duracion=21'12" | ||
| + | |url1=https://www.youtube.com/watch?v=jCDBKO8ghtg&list=PLZNmE9BEzVIkfJ32AmaQoob2npxScGpo3&index=5 | ||
| + | |sinopsis=Tutorial en el que se trabaja con las funciones definidas por partes en fórmulas, cálculo de imágenes y preimágenes de valores. | ||
| + | }} | ||
| + | {{Video_enlace_clasematicas | ||
| + | |titulo1=Tutorial 1b | ||
| + | |duracion=17'02" | ||
| + | |url1=https://www.youtube.com/watch?v=KOXcDbcfj44&index=6&list=PLZNmE9BEzVIk3VQdqC9kJ8pcR0iJJMh87 | ||
| + | |sinopsis=Tutorial en el que se representa gráficamente funciones definidas por partes en fórmulas. | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=5'39" | ||
| + | |sinopsis=Halla el valor de f(-10) en la siguiente función a trozos: | ||
| - | {{ai_cuerpo | + | :<math>f(x) = \begin{cases} t^2-5t & \mbox{si } t \le -10 \\ t+19 & \mbox{si } -10<t<-2 \\ \cfrac{t^3}{t+9} & \mbox{si } x \ge -2 \end{cases}</math> |
| - | |enunciado='''Actividad 1.''' Representación gráfica de funciones definidas en dos trozos. | + | |
| - | |actividad=Puedes modificar la definicion de la función en la ventana de la izquierda. | + | |
| - | Utiliza e deslizador para modificar el punto de cambio. | + | |url1=https://youtu.be/TSuuXnT7QMc |
| - | <center><iframe> | + | }} |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/f_trozos_1.html | + | {{Video_enlace_khan |
| - | width=780 | + | |titulo1=Ejercicio 2 |
| - | height=460 | + | |duracion=7'32" |
| - | name=myframe | + | |sinopsis=Obtén la expresión analítica de la función a trozos a partir de su gráfica dada en el video. |
| - | </iframe></center> | + | |url1=https://youtu.be/6X_7SU2fy00 |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/f_trozos_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | }} |
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=13'38" | ||
| + | |sinopsis=Obtén la gráfica, el dominio y el rango de la siguiente función a trozos: | ||
| + | |||
| + | :<math>f(x) = \begin{cases} x^2+2x & \mbox{si }x \le 1 \\ ~~x & \mbox{si } -1 < x \le 1 \\ -1 & \mbox{si } x>1 \end{cases}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=AU1GVkYD78w | ||
| }} | }} | ||
| - | {{ai_cuerpo | + | {{Video_enlace_unicoos |
| - | |enunciado='''Actividad 2.''' Representación gráfica de funciones definidas en tres trozos. | + | |titulo1=Ejercicio 4 |
| - | |actividad=Puedes modificar la definicion de la función en la ventana de la izquierda. | + | |duracion=4'51" |
| + | |sinopsis=La '''función signo''' viene dada por la siguiente expresión: | ||
| - | Utiliza los deslizadores para modificar los puntos de cambio. | + | :<math>sgn(x) = \begin{cases} -1 & \mbox{si } x < 0 \\ 0 & \mbox{si } x=0 \\ 1 & \mbox{si } x>0 \end{cases}</math> |
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/geogebra/figuras/f_trozos_2.html | + | |
| - | width=780 | + | |
| - | height=460 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/f_trozos_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |
| + | Teniendo en cuenta esto representa: <math>y=sgn(4x-2)\;</math>. | ||
| + | |||
| + | |url1=http://www.unicoos.com/video/matematicas/4-eso/funciones-elementales/funcion-signo/funcion-signo-01 | ||
| }} | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 5 | ||
| + | |duracion=6'26" | ||
| + | |sinopsis=Representa gráficamente la función a trozos: | ||
| + | :<math>f(x) = \begin{cases} -0.125x+4.75 & \mbox{si } -10 \le x < -2 \\ \qquad x+7 & \mbox{si } ~-2 \le x < -1 \\ \quad \cfrac{12}{11}x+\cfrac{54}{11} & \mbox{si } ~-1 \le x \le 10 \end{cases}</math> | ||
| + | |||
| + | |url1=https://youtu.be/Gf1r578-E10 | ||
| }} | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 6 | ||
| + | |duracion=3'22" | ||
| + | |sinopsis=Halla el dominio y el rango de la siguiente función a trozos: | ||
| + | |||
| + | :<math>f(x) = \begin{cases} ~1 & \mbox{si } 0 < x \le 2 \\ ~5 & \mbox{si } 2 < x < 6 \\ -7 & \mbox{si } 6 \le x \le 11 \end{cases}</math> | ||
| + | |||
| + | |url1=https://youtu.be/mvsTzLxMGdc | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 7 | ||
| + | |duracion=9'41" | ||
| + | |sinopsis=Halla el dominio y el rango de la siguiente función a trozos: | ||
| + | |||
| + | :<math>f(x) = \begin{cases} x+7 & \mbox{si } -6 < x \le -3 \\ 1-x & \mbox{si } -3 < x < 4 \\ 2x-11 & \mbox{si } ~4 \le x \le 6 \end{cases}</math> | ||
| + | |||
| + | |url1=https://youtu.be/3i7ZQ13ocI4 | ||
| + | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Funciones definidas a trozos|enunciado= | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1a | ||
| + | |descripcion=Evaluar funciones definidas por partes | ||
| + | |url1=http://es.khanacademy.org/math/algebra/absolute-value-equations-functions/piecewise-functions/e/evaluating-piecewise-functions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1b | ||
| + | |descripcion=Evaluar funciones definidas por partes | ||
| + | |url1=http://es.khanacademy.org/math/algebra/absolute-value-equations-functions/piecewise-functions/e/evaluate-step-functions-from-their-graph | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 2 | ||
| + | |descripcion=Representa gráficamente funciones definidas por partes | ||
| + | |url1=http://es.khanacademy.org/math/algebra/absolute-value-equations-functions/piecewise-functions/e/piecewise-graphs-linear | ||
| + | }} | ||
| + | }} | ||
| + | |||
| {{p}} | {{p}} | ||
Revisión actual
Una función definida a trozos es aquella que utiliza varias funciones para su definición, cada una de ellas definida en un determinado subconjunto del dominio de definición de la función principal.
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Ejemplos: Función definida a trozos
Representa la siguiente función:
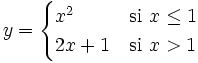
Ejemplos: Función definida a trozos
Tendremos que hallar las ecuaciones de tres rectas. Para ello localizaremos dos puntos por los que pase cada recta y a partir de ellos obtendremos su pendiente y luego su ecuación por medio de la ecuación punto-pendiente.

Tutorial en el que se trabaja con las funciones definidas por partes en fórmulas, cálculo de imágenes y preimágenes de valores.
Tutorial en el que se representa gráficamente funciones definidas por partes en fórmulas.
Halla el valor de f(-10) en la siguiente función a trozos:
Obtén la expresión analítica de la función a trozos a partir de su gráfica dada en el video.
Obtén la gráfica, el dominio y el rango de la siguiente función a trozos:
La función signo viene dada por la siguiente expresión:
Teniendo en cuenta esto representa: 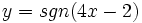 .
.
Representa gráficamente la función a trozos:
Halla el dominio y el rango de la siguiente función a trozos:
Halla el dominio y el rango de la siguiente función a trozos:
Evaluar funciones definidas por partes
Evaluar funciones definidas por partes
Representa gráficamente funciones definidas por partes