Plantilla:Valor numérico de un polinomio
De Wikipedia
| Revisión de 09:15 12 ene 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:27 12 ene 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 31: | Línea 31: | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| |titulo1=Ejercicio 4 | |titulo1=Ejercicio 4 | ||
| - | |duracion=13'12" | + | |duracion=5'13" |
| - | |sinopsis=Ejercicios 7 y 8: Clasificar polinomios en homogéneos/heterogéneos. Calcular el valor numérico | + | |sinopsis=8) Calcula el valor numérico de los siguientes polinomios para el valor de la variable indicado: |
| - | |url1=https://www.youtube.com/watch?v=wXujh2wQNnE&index=6&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHxhttps://www.youtube.com/watch?v=A3AuZovTSQ4&list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx&index=7 | + | |
| + | :a) <math>P(x)=3x^2+2x-6\;</math> para <math>x=2\;</math> | ||
| + | |||
| + | :b) <math>P(x)=5x-7\;</math> para <math>x=-3\;</math> | ||
| + | |||
| + | :c) <math>2x^3-3x^2+4x-2\;</math> para <math>x=-1\;</math> | ||
| + | |||
| + | :d) <math>6x^2+3\;</math> para <math>x=9\;</math> | ||
| + | |||
| + | :e) <math>-2x^3+5x^2-2x\;</math> para <math>x=-2\;</math> | ||
| + | |||
| + | |url1=https://youtu.be/A3AuZovTSQ4?list=PLw7Z_p6_h3ownxKVgYhDK54I8HcRpwGHx&t=315 | ||
| }} | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
Revisión de 09:27 12 ene 2018
Si en un polinomio se sustituyen las letras por números y se realiza la operación indicada se obtiene un número que es el valor númerico del polinomio para los valores de las letras dados.
Tutorial 1 (6'17") Sinopsis: Aprende a calcular el valor numérico de un polinomio
Ejercicio 1 (3'59") Sinopsis: Halla el valor numérico del polinomio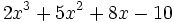 
cuando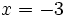 
Ejercicio 2 (5'31") Sinopsis: Dado el polinomio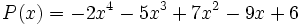 
, determina 
.
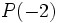Ejercicio 3 (4'58") Sinopsis: Halla el valor numérico del polinomio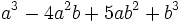 
cuando 
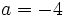y 
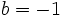
Ejercicio 4 (5'13") Sinopsis: 8) Calcula el valor numérico de los siguientes polinomios para el valor de la variable indicado:
- a)
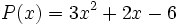para 
- b)
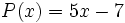para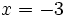
- c)
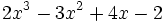para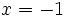 
- d)
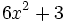para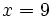 
- e)
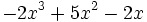para 
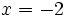
Ejercicio 5 (2'46") Sinopsis: Evalúa el polinomio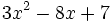 
en .
Ejemplos Descripción: Distintas situaciones en las que se hace uso del valor numérico de un polinomio. Por ejemplo, cuando se expresa un número en un sistema de numeración de una determinada base.
Actividades Descripción: Actividades en las que deberás calcular el valor numérico de un polinomio.
Un número se dice que es una raíz de un polinomio si el valor numérico del polinomio para dicho número es cero.
Veamos como el número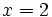 
es una raíz del polinomio 
.
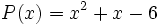En efecto, al sustituir la x por 2, el valor numérico del polinomio es cero: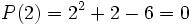 
Actividad: Valor numérico y raíces de un polinomio Calcula el valor numérico del polinomio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
De a) y c) se deduce que x=2 y x=1 son raíces del polinomio. Prueba a introducir lo siguiente: roots x^2-3x+2 |
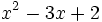en los casos:
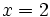b) 
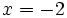c) 
