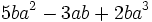Plantilla:Sacar factor común
De Wikipedia
| Revisión de 09:45 17 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto='''Sacar factor común''' en una expresión algebraica con varios sumandos, consiste en encontrar una parte común a todos esos sumandos y aplicar la propiedad distributiva para poner la expresión algebraica como producto de esa parte común y una serie de sumandos entre paréntesis.}} | + | Otra herramienta básica para la descomposición y simplificación de expresiones algebraicas es la de sacar factor común. La idea es transformar una expresión compleja en un producto de expresiones más sencillas. |
| {{p}} | {{p}} | ||
| - | {{Ejemplo | + | {{Definición y ejemplos: Sacar factor común}} |
| - | |titulo=Ejemplo: ''Sacar factor común'' | + | |
| - | |enunciado= | + | |
| - | Saca factor común en la expresión <math>16xyz-24xz+4x\;\!</math> | + | |
| - | |sol= | + | |
| - | El factor común, que se repite en los tres sumandos, es <math>4x\,\!</math>. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común <math>4x\,\!</math>, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:{{p}} | + | |
| - | <center><math>16xyz-24xz+4x\;\!=</math>{{p}} | + | |
| - | <math>(4x) \cdot 4yz - (4x) \cdot 6z + (4x) \cdot 1=\;\!</math>{{p}} | + | |
| - | <math>4x \cdot (4yz-6z+1)</math></center> | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Videotutoriales|titulo=Sacar factor común|enunciado= | + | {{Videos: Sacar factor común}} |
| - | {{Video_enlace | + | {{Actividades: Sacar factor común}} |
| - | |titulo1=Ejemplos 1: Sacar factor común | + | {{Videos: Sacar factor común por agrupación}} |
| - | |duracion=7'18" | + | {{Wolfram: Sacar factor común}} |
| - | |sinopsis=Saca factor común: | + | |
| - | + | ||
| - | a) <math>ax+bx\;</math> | + | |
| - | + | ||
| - | b) <math>9x^3-24x^2\;</math> | + | |
| - | + | ||
| - | c) <math>2x^2y+6xy^2-8x^2y^2\;</math> | + | |
| - | + | ||
| - | d) <math>3x^2y-3x^2z+3x^2\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=N5xGLmx9oHE | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| - | {{Video_enlace_julioprofe | + | {{ejercicio |
| - | |titulo1=Ejemplos 2: Sacar factor común | + | |titulo=Ejercicios: ''Sacar factor común'' |
| - | |duracion=6'09" | + | |cuerpo= |
| - | |sinopsis=Saca factor común: | + | |
| - | a) <math>3x+3y\;</math> | ||
| - | |||
| - | b) <math>10a-15b\;</math> | ||
| - | |||
| - | c) <math>4pq-8pr+12pt\;</math> | ||
| - | |||
| - | d) <math>x(a+1)-t(a+1)+5(a+1)\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=LWyZSXsMAr8&index=47&list=PL9B9AC3136D2D4C45 | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_unicoos | ||
| - | |titulo1=Ejemplos 3: Sacar factor común | ||
| - | |duracion=22'35" | ||
| - | |sinopsis=Saca factor común: | ||
| - | |||
| - | a) <math>8a-4b+16c+12d\;</math> | ||
| - | |||
| - | b) <math>7x^2+11x^3-4x^5+3x^4-x^8\;</math> | ||
| - | |||
| - | c) <math>9x^3-6x^2+12x^5-16x^7\;</math> | ||
| - | |||
| - | d) <math>\frac{4}{3}x-\frac{8}{9}x^3+\frac{16}{15}x^7-\frac{2}{3}x^5\;</math> | ||
| - | |||
| - | e) <math>9x^2ab-3xa^2b^3+x^2az\;</math> | ||
| - | |||
| - | f) <math>3(x+1)-5x(x+1)+x^2(x+1)\;</math> | ||
| - | |url1=http://www.unicoos.com/video/matematicas/2-eso/expresiones-algebraicas/polinomios/factor-comun | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| - | {{Video_enlace | ||
| - | |titulo1=Ejemplos 4: Sacar factor común | ||
| - | |duracion=9'27" | ||
| - | |sinopsis=Saca factor común: | ||
| - | |||
| - | a) <math>2(a+b)+x(a+b)\;</math> | ||
| - | |||
| - | b) <math>(x+y)a-(x+y)b-x-y\;</math> | ||
| - | |||
| - | c) <math>ax-bx+cx+ay-by+cy-a+b-c\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=JjbFpdlwPW8 | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplos 5: Sacar factor común por agrupación de términos | ||
| - | |duracion=7'08" | ||
| - | |sinopsis=Saca factor común: | ||
| - | |||
| - | a) <math>px+mx+py+my\;</math> | ||
| - | |||
| - | b) <math>2ac-5bd-2a+2ad+5b-5bc\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=uhN2eVLAEDw&index=48&list=PL9B9AC3136D2D4C45}} | ||
| - | {{p}} | ||
| - | |||
| - | {{Video_enlace | ||
| - | |titulo1=Ejemplos 6: Sacar factor común por agrupación de términos | ||
| - | |duracion=12'37" | ||
| - | |sinopsis=3 ejemplos. | ||
| - | |url1=https://www.youtube.com/watch?v=HLb7Wmx-1_c | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | {{wolfram desplegable|titulo=Sacar factor común|contenido= | ||
| - | {{wolfram | ||
| - | |titulo=Actividad: ''Sacar factor común'' | ||
| - | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | :Saca factor común: | ||
| - | :a) <math>3x^2yz-6xy^2z+9xyz\!</math> | + | '''1. '''Extrae factor común: |
| - | :b) <math>12ab^5-6a^4b^3\!</math> | + | |
| - | {{p}} | + | :a) <math>-18a+20a-10a\,\!</math> {{b4}} b) <math>15x-60x^2\,\!</math> {{b4}} c) <math>5ba^2-3ab+2ba^3\;\!</math> |
| + | <p></p> | ||
| |sol= | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | a) <math>-8a\,\!</math>{{b4}} b) <math>15x \cdot (1-4x)\,\!</math>{{b4}}c) <math>ab \cdot (5a-3+2a^2)</math> |
| - | + | ||
| - | a) {{consulta|texto=factor 3x^2*y*z-6x*y^2*z+9x*y*z}} | + | |
| - | b) {{consulta|texto=factor 12a*b^5-6a^4*b^3}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| - | }} | + | |
| }} | }} | ||
| }} | }} | ||
| + | {{p}} | ||
Revisión actual
Otra herramienta básica para la descomposición y simplificación de expresiones algebraicas es la de sacar factor común. La idea es transformar una expresión compleja en un producto de expresiones más sencillas.
Sacar factor común en una expresión algebraica con varios sumandos, consiste en encontrar una parte común a todos esos sumandos y aplicar la propiedad distributiva para poner la expresión algebraica como producto de esa parte común y una serie de sumandos entre paréntesis.
Ejemplo: Sacar factor común
Saca factor común en la expresión 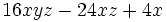
El factor común, que se repite en los tres sumandos, es
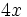 . Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común
. Ese factor lo multiplicamos por un paréntesis que contenga a otros tres sumandos. Cada uno de los sumandos del paréntesis deberá ser tal, que al multiplicarlo por el factor común 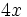 , dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
, dé como resultado cada uno de los sumandos de la expresión de partida. En nuestro caso:
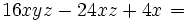
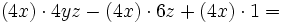
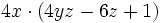
Cómo se saca factor común. Ejemplos
- En este tutorial se explica la extracción de factor común en expresiones algrebraicas, el caso más sencillo de factorización de polinomios.
- (4:40) La propiedad distributiva. Demostración geométrica.
Sacara factor común.
Saca factor común:
a) 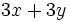
b) 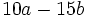
c) 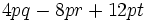
d) 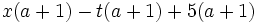
Saca factor común:
a) 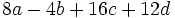
b) 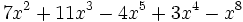
c) 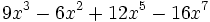
d) 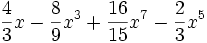
e) 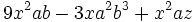
f) 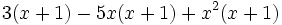
Saca factor común:
a) 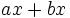
b) 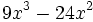
c) 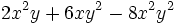
d) 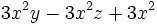
Saca factor común:
a) 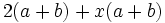
b) 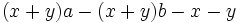
c) 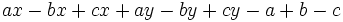
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
Saca factor común:
- a)
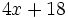
- b)
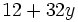
Saca factor común:
Saca factor común:
El área de un rectángulo es de 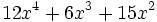 y su largo es el m.c.d. de cada uno de los sumandos del anterior polinomio. Calcula las dimensiones del rectángulo.
y su largo es el m.c.d. de cada uno de los sumandos del anterior polinomio. Calcula las dimensiones del rectángulo.
Saca factor común:
- Sabiendo que
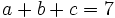 , calcula
, calcula 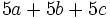 .
.
- Sabiendo que
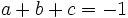 y que
y que 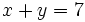 , calcula
, calcula 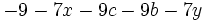 .
.
- Sabiendo que
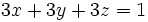 , calcula
, calcula 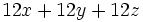 .
.
- Sabiendo que
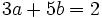 , calcula
, calcula  .
.
Actividades para aprender y practicar cómo se saca factor común.
Factorizar polinomios sacando factor común.
Factorizar polinomios sacando factor común.
Evalúa expresiones usando la estructura.
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
a) 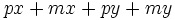
b) 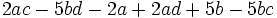
Saca factor común por agrupación de términos:
a) 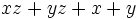
b) 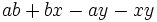
c) 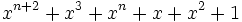
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
Saca factor común por agrupación de términos:
|
Ejercicios: Sacar factor común 1. Extrae factor común:
Solución: a) 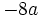 b) b) 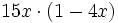 c) c) 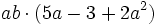 |
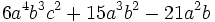
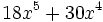
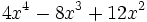
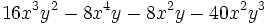
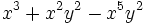
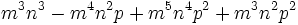
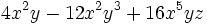
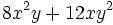
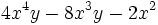
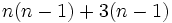
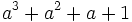
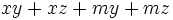
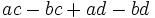
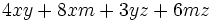
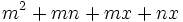
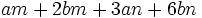
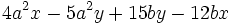
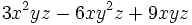
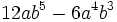
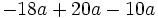 b)
b) 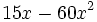 c)
c)