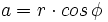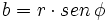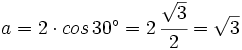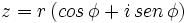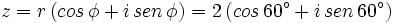Números complejos: Forma polar (1ºBach)
De Wikipedia
| Revisión de 15:30 4 oct 2016 Coordinador (Discusión | contribuciones) (→Forma polar de un número complejo) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Familias de complejos en forma polar) |
||
| Línea 5: | Línea 5: | ||
| |enlaces= | |enlaces= | ||
| }} | }} | ||
| + | __TOC__ | ||
| {{p}} | {{p}} | ||
| + | (Pág. 152) | ||
| ==Forma polar de un número complejo== | ==Forma polar de un número complejo== | ||
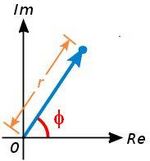
| {{Tabla75|celda2=[[Imagen:complejopolar.jpg|thumb|150px|Fig. 1: Un número complejo queda determinado por su módulo y su argumento.]]|celda1= | {{Tabla75|celda2=[[Imagen:complejopolar.jpg|thumb|150px|Fig. 1: Un número complejo queda determinado por su módulo y su argumento.]]|celda1= | ||
| Línea 12: | Línea 14: | ||
| *El '''módulo''' de <math>z\,</math> es la longitud del vector que lo representa, es decir, la distancia entre el afijo <math>(a,b)\,</math> y el origen <math>(0,0)\,)</math>. Se designa por <math>r=|z|\,</math>. | *El '''módulo''' de <math>z\,</math> es la longitud del vector que lo representa, es decir, la distancia entre el afijo <math>(a,b)\,</math> y el origen <math>(0,0)\,)</math>. Se designa por <math>r=|z|\,</math>. | ||
| - | *El '''argumento''' de <math>z\,</math> (<math>z \ne 0</math>), es el ángulo que forma el vector con el eje X . Se designa por <math>\phi=arg(z)\,</math>. | + | *El '''argumento''' de <math>z\,</math> (<math>z \ne 0</math>), es el ángulo que forma el vector con el eje X . Se designa por <math>\phi=arg(z)\,</math>. De los infinitos argumentos de un número complejo, al comprendido entre 0º y 360º se le llama '''argumento principal'''. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=La '''forma polar''' del número complejo <math>z \, (z \ne 0)</math>, se designa <math>r_\phi \,</math>, siendo <math>r=|z|\,</math> y <math>\phi=arg(z)\,</math>.}} | + | {{Caja_Amarilla|texto=La '''forma polar''' del número complejo <math>z \, (z \ne 0)</math>, se designa <math>r_\phi \,</math>, siendo <math>r=|z|\,</math> y <math>\phi=arg(z)\,</math>. |
| + | |||
| + | (El cero, al no tener argumento, no se puede poner en forma polar) | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| + | Si <math>z= r_\phi\;</math>, entonces: | ||
| + | |||
| + | *Su '''opuesto''' es <math>-z=r_{\phi + 180^\circ}</math> | ||
| + | *Su '''conjugado''' es <math>\bar z = r_{-\phi}</math> | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver como se representan los números complejos en forma polar. Mueve el deslizador para ver algunos ejemplos y completa los que faltan en tu cuaderno. | ||
| + | |enlace=[https://ggbm.at/jn7FC8yA Forma polar de números complejos] | ||
| }} | }} | ||
| ==Paso de forma binómica a polar== | ==Paso de forma binómica a polar== | ||
| - | {{Teorema|titulo=Proposición|enunciado= | + | {{Teorema|titulo=Procedimiento|enunciado= |
| Dado un número complejo <math>z=a+bi\,</math> su forma polar <math>r_\phi \,</math> se obtiene de la siguiente manera: | Dado un número complejo <math>z=a+bi\,</math> su forma polar <math>r_\phi \,</math> se obtiene de la siguiente manera: | ||
| Línea 34: | Línea 51: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Paso de forma binómica a polar'' | {{Ejemplo|titulo=Ejemplo: ''Paso de forma binómica a polar'' | ||
| - | |enunciado=:Pasa a forma polar el número complejo <math>z=2+2i\,</math> | + | |enunciado=Pasa a forma polar: |
| + | :a) <math>z=2+2i\,</math> | ||
| + | :b) <math>z=-i\,</math> | ||
| + | :c) <math>z=-3\,</math> | ||
| |sol= | |sol= | ||
| - | :Calculamos el módulo: | + | a) <math>z=2+2i\,</math> |
| - | ::<math>r = |z| = \sqrt{2^2+2^2}=\sqrt{8}</math> | + | |
| - | :Calculamos el argumento: | + | |
| - | ::<math>\phi=arctg \, \cfrac{2}{2}=45^\circ</math> | + | |
| - | :Por tanto, su forma polar es: | + | Calculamos el módulo: |
| + | :<math>r = |z| = \sqrt{2^2+2^2}=\sqrt{8}</math> | ||
| + | Calculamos el argumento: | ||
| + | :<math>\phi=arctg \, \cfrac{2}{2}=45^\circ</math> | ||
| - | ::<math>z=\sqrt{8}_{45^\circ}</math> | + | '''Solución:''' <math>z=(\sqrt{8})_{45^\circ}</math> |
| + | ---- | ||
| + | b) <math>z=-i\,</math> | ||
| + | |||
| + | '''Solución:''' <math>z=1_{270^\circ}</math> | ||
| + | ---- | ||
| + | c) <math>z=-3\,</math> | ||
| + | |||
| + | '''Solución:''' <math>z=3_{180^\circ}</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Paso de forma binómica a polar''|cuerpo= | + | {{Video_enlace_8cifras |
| - | {{ai_cuerpo | + | |titulo1=De forma binómica a forma polar |
| - | |enunciado=:Pasa los siguientes números complejos a forma polar y comprueba tus resultados en la escena: | + | |duracion=14´50" |
| + | |url1=https://www.youtube.com/watch?v=YQuDN2MUKkk&index=7&list=PLpbLLqs33gIlut1lGHmwYqQjl6-yDrsPf | ||
| + | |sinopsis=Qué es la forma polar de un número complejo, y cómo se pasa de forma binómica a polar. | ||
| + | }} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Paso de forma binómica a polar | ||
| + | |descripcion=Pasa los siguientes números complejos a forma polar y comprueba tus resultados en la escena: | ||
| ::'''a)'''<math>1+2i\,</math>{{b4}} '''b)'''<math>-2+3i\,</math>{{b4}} c) <math>-3-i\,</math> {{b4}} '''d)'''<math>5-4i\,</math> | ::'''a)'''<math>1+2i\,</math>{{b4}} '''b)'''<math>-2+3i\,</math>{{b4}} c) <math>-3-i\,</math> {{b4}} '''d)'''<math>5-4i\,</math> | ||
| {{p}} | {{p}} | ||
| - | |actividad= | ||
| En esta escena puedes pasar un complejo de forma binómica a polar. Puedes variar los valores de a y b o mover el afijo con el ratón. | En esta escena puedes pasar un complejo de forma binómica a polar. Puedes variar los valores de a y b o mover el afijo con el ratón. | ||
| Línea 58: | Línea 91: | ||
| url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_1.html | url=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_1.html | ||
| width=430 | width=430 | ||
| - | height=390 | + | height=450 |
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_1.html '''Click''' aquí si no se ve bien la escena]</center> | + | |url1=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_1.html |
| + | }} | ||
| + | {{p}} | ||
| + | {{wolfram desplegable|titulo=Paso de forma binómica a polar|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Paso de forma binómica a polar'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | a) Pasa <math>1-i\;</math> a forma polar. | ||
| + | |||
| + | b) Halla el argumento de <math>1-i\;</math>. | ||
| + | |||
| + | b) Halla el módulo de <math>1-i\;</math>. | ||
| + | |||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | a) {{consulta|texto=convert 1-i to polar form}} | ||
| + | |||
| + | b) {{consulta|texto=arg (1-i) in degrees}} o {{consulta|texto=arg (1-i)}} | ||
| + | |||
| + | c) {{consulta|texto=<math>|1-i|</math>}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | (Pág. 153) | ||
| ==Paso de forma polar a binómica== | ==Paso de forma polar a binómica== | ||
| - | {{Caja_Amarilla|texto= | + | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= |
| Dado un número complejo <math>r_\phi \,</math>, su forma binómica <math>a+bi\,</math> se obtiene de la siguiente manera: | Dado un número complejo <math>r_\phi \,</math>, su forma binómica <math>a+bi\,</math> se obtiene de la siguiente manera: | ||
| Línea 77: | Línea 136: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Paso de forma polar a binómica'' | {{Ejemplo|titulo=Ejemplo: ''Paso de forma polar a binómica'' | ||
| - | |enunciado=:Pasa a forma binómica el número complejo <math>z=2_{30^\circ}</math> | + | |enunciado=Pasa a forma binómica el número complejo <math>z=2_{30^\circ}</math> |
| |sol= | |sol= | ||
| - | :Calculamos la parte real: | + | Calculamos la parte real: |
| - | ::<math>a=2 \cdot cos \, 30^\circ=2 \, \cfrac{\sqrt{3}}{2}=\sqrt{3}</math> | + | :<math>a=2 \cdot cos \, 30^\circ=2 \, \cfrac{\sqrt{3}}{2}=\sqrt{3}</math> |
| - | :Calculamos su parte imaginaria: | + | Calculamos su parte imaginaria: |
| - | ::<math>b=2 \cdot sen \, 30^\circ=2 \, \cfrac{1}{2}=1</math> | + | :<math>b=2 \cdot sen \, 30^\circ=2 \, \cfrac{1}{2}=1</math> |
| - | + | ||
| - | :Por tanto, su forma binómica es: | + | |
| - | ::<math>z=\sqrt{3}+i</math> | + | '''Solución:''' <math>z=\sqrt{3}+i</math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Paso de forma polar a binómica''|cuerpo= | + | {{Video_enlace_8cifras |
| - | {{ai_cuerpo | + | |titulo1=De forma polar a binómica |
| - | |enunciado=:Pasa los siguientes números complejos a forma binómica y comprueba tus resultados en esta escena: | + | |duracion=9´12" |
| + | |url1=https://www.youtube.com/watch?v=IK1SaP8uvVM&index=8&list=PLpbLLqs33gIlut1lGHmwYqQjl6-yDrsPf | ||
| + | |sinopsis=Cómo se pasa un complejo de forma polar a binómica. | ||
| + | }} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Paso de forma polar a binómica | ||
| + | |descripcion=Pasa los siguientes números complejos a forma binómica y comprueba tus resultados en esta escena: | ||
| ::'''a)'''<math>1_{225^\circ}</math>{{b4}} '''b)'''<math>4_{0^\circ}</math> {{b4}} '''c)''' <math>3_{270^\circ}</math>{{b4}} '''d)'''<math>2_{295^\circ}</math> {{b4}}'''e)'''<math>8_{90^\circ}</math> {{b4}}'''f)'''<math>2_{120^\circ}</math> | ::'''a)'''<math>1_{225^\circ}</math>{{b4}} '''b)'''<math>4_{0^\circ}</math> {{b4}} '''c)''' <math>3_{270^\circ}</math>{{b4}} '''d)'''<math>2_{295^\circ}</math> {{b4}}'''e)'''<math>8_{90^\circ}</math> {{b4}}'''f)'''<math>2_{120^\circ}</math> | ||
| {{p}} | {{p}} | ||
| - | |actividad= | ||
| En esta escena puedes pasar un complejo de forma polar a binómica. Puedes variar los valores del módulo y del argumento. | En esta escena puedes pasar un complejo de forma polar a binómica. Puedes variar los valores del módulo y del argumento. | ||
| Línea 104: | Línea 166: | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_2.html '''Click''' aquí si no se ve bien la escena]</center> | + | |url1=http://maralboran.org/web_ma/descartes/Bach_CNST_1/Los_numeros_complejos/complejos4_2.html |
| - | + | ||
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 124: | Línea 184: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo|titulo=Ejemplo: ''Forma trigonométrica de un complejo'' | {{Ejemplo|titulo=Ejemplo: ''Forma trigonométrica de un complejo'' | ||
| - | |enunciado=:Pasa a forma trigonométrica el número complejo <math>z=2_{60^\circ}</math> | + | |enunciado=Pasa a forma trigonométrica el número complejo <math>z=2_{60^\circ}</math> |
| |sol= | |sol= | ||
| - | :Tan sólo hay que aplicar la fórmula: | + | Tan sólo hay que aplicar la fórmula: |
| - | ::<math>z=r \, (cos \, \phi + i \, sen \, \phi)=2 \, (cos \, 60^\circ + i \, sen \, 60^\circ) </math> | + | :<math>z=r \, (cos \, \phi + i \, sen \, \phi)=2 \, (cos \, 60^\circ + i \, sen \, 60^\circ) </math> |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Videotutoriales|titulo=Formas polar y trigonométrica de un número complejo|enunciado= |
| - | |titulo1= Formas polar y trigonométrica de un número complejo | + | {{Video_enlace_fonemato |
| + | |titulo1=Tutorial | ||
| |duracion=11´22" | |duracion=11´22" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/07-formas-polar-y-trigonometrica-de-un-numero-complejo#.VCryRRa7ZV8 | + | |url1=https://www.youtube.com/watch?v=azuVR4S0UD0&list=PLB2E59B57C33C7B8D&index=16 |
| |sinopsis=Videotutorial. | |sinopsis=Videotutorial. | ||
| }} | }} | ||
| - | {{p}} | + | ---- |
| - | {{ejercicio | + | {{Video_enlace_fonemato |
| - | |titulo=Ejercicios:''Formas polar y trigonométrica de un número complejo'' | + | |titulo1= Ejercicio 1 |
| - | |cuerpo= | + | |
| - | {{Video_enlace | + | |
| - | |titulo1= 4 ejercicios | + | |
| |duracion=10´34" | |duracion=10´34" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/0701-cuatro-ejercicios-5#.VCry0Ba7ZV8 | + | |url1=https://www.youtube.com/watch?v=BYOUqBDau1c&list=PLB2E59B57C33C7B8D&index=17 |
| - | |sinopsis=Videotutorial. | + | |sinopsis=4 ejercicios. |
| }} | }} | ||
| - | {{Video_enlace | + | {{Video_enlace_fonemato |
| - | |titulo1= 4 ejercicios | + | |titulo1=Ejercicio 2 |
| - | |duracion=7´ | + | |duracion=7´00" |
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/0702-cuatro-ejercicios-2#.VCrzBha7ZV8 | + | |url1=https://www.youtube.com/watch?v=7agSOtjzFvQ&list=PLB2E59B57C33C7B8D&index=18 |
| - | |sinopsis=Videotutorial. | + | |sinopsis=4 ejercicios |
| }} | }} | ||
| - | {{Video_enlace | + | {{Video_enlace_fonemato |
| - | |titulo1= 9 ejercicios | + | |titulo1=Ejercicio 3 |
| |duracion=10´37" | |duracion=10´37" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/12-numeros-complejos/0703-nueve-ejercicios#.VCrzLxa7ZV8 | + | |url1=https://www.youtube.com/watch?v=d2qfqSWpPXg&list=PLB2E59B57C33C7B8D&index=25 |
| - | |sinopsis=Videotutorial. | + | |sinopsis=9 ejercicios. |
| }} | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| + | ==Familias de complejos en forma polar== | ||
| + | |||
| + | {{Ejemplo|titulo=Ejercicio resuelto: ''Familias de complejos en forma polar'' | ||
| + | |enunciado=Representa los siguientes conjuntos de números complejos: | ||
| + | |||
| + | :a) <math>|z|=3\;</math> | ||
| + | |||
| + | :b) <math>|z|<3\;</math> | ||
| + | |||
| + | :c) <math>1 \le |z| \le 3</math> | ||
| + | |||
| + | :d) <math>Arg(z)=30^\circ</math> | ||
| + | |sol= | ||
| + | :'''a)''' Como <math>|z|=3\;</math>, los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es igual a 3, esto es, una circunferencia de centro O y radio 3. | ||
| + | |||
| + | :'''b)''' Como <math>|z|<3\;</math>, los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es menor que 3, esto es, una círculo de centro O y radio 3 sin la circunferencia del borde. | ||
| + | |||
| + | :'''c)''' Como <math>1 \le |z| \le 3</math>, la solución es una corona circular de radios 1 y 3 y centro O, incluidas las circunferencias de los bordes. | ||
| + | |||
| + | :'''d)''' Como <math>Arg(z)=30^\circ</math> la solución es una semirrecta abierta de origen O que forma un ángulo de 30º con el eje X. | ||
| + | |||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena de Geogebra podrás ver como se representan gráficamente las soluciones. | ||
| + | |enlace=[http://ggbm.at/DWpDZeYY Soluciones] | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ==Ejercicios== | ||
| + | ===Ejercicios propuestos=== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Forma polar de un número complejo'' | ||
| + | |cuerpo= | ||
| + | (Pág. 153) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 2a,e,f; 3a,e,f; 4; 5; 6 | ||
| + | |||
| + | [[Imagen:yellow_star.png|12px]] 1; 2b,c,d; 3b,c,d | ||
| + | |||
| + | (Pág. 158) | ||
| + | |||
| + | [[Imagen:red_star.png|12px]] 1c,d,e; 2d,e | ||
| + | |||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 152)
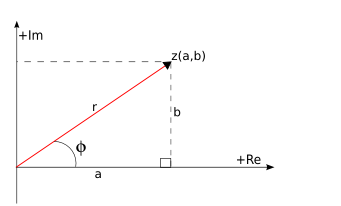
Forma polar de un número complejo
Dado un número complejo
La forma polar del número complejo (El cero, al no tener argumento, no se puede poner en forma polar) |
En esta escena podrás ver como se representan los números complejos en forma polar. Mueve el deslizador para ver algunos ejemplos y completa los que faltan en tu cuaderno.
Paso de forma binómica a polar
Procedimiento
Dado un número complejo 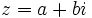 su forma polar
su forma polar 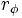 se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
| 
|
Ejemplo: Paso de forma binómica a polar
Pasa a forma polar:
- a)
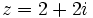
- b)
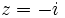
- c)
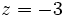
a) 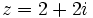
Calculamos el módulo:
Calculamos el argumento:
Solución: 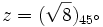
b) 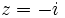
Solución: 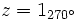
c) 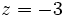
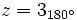
Qué es la forma polar de un número complejo, y cómo se pasa de forma binómica a polar.
Pasa los siguientes números complejos a forma polar y comprueba tus resultados en la escena:
- a)
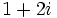 b)
b)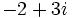 c)
c) 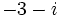 d)
d)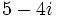
- a)
En esta escena puedes pasar un complejo de forma binómica a polar. Puedes variar los valores de a y b o mover el afijo con el ratón.
|
Actividad: Paso de forma binómica a polar a) Pasa b) Halla el argumento de b) Halla el módulo de Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) convert 1-i to polar form b) arg (1-i) in degrees o arg (1-i) c) | 1 − i | |
(Pág. 153)
Paso de forma polar a binómica
Ejemplo: Paso de forma polar a binómica
Pasa a forma binómica el número complejo 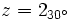
Calculamos la parte real:
Calculamos su parte imaginaria:
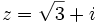
Cómo se pasa un complejo de forma polar a binómica.
Pasa los siguientes números complejos a forma binómica y comprueba tus resultados en esta escena:
- a)
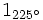 b)
b)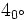 c)
c) 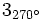 d)
d)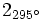 e)
e)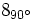 f)
f)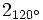
- a)
En esta escena puedes pasar un complejo de forma polar a binómica. Puedes variar los valores del módulo y del argumento.
Forma trigonométrica de un número complejo
Según lo visto en el apartado anterior:
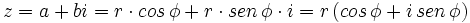
Se llama forma trigonométrica de un número complejo, a la expresión
|
|
Ejemplo: Forma trigonométrica de un complejo
Pasa a forma trigonométrica el número complejo 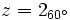
Tan sólo hay que aplicar la fórmula:
Videotutorial.
4 ejercicios.
4 ejercicios
9 ejercicios.
Familias de complejos en forma polar
Ejercicio resuelto: Familias de complejos en forma polar
Representa los siguientes conjuntos de números complejos:
- a)
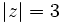
- b)
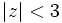
- c)
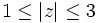
- d)
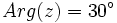
- a) Como
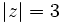 , los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es igual a 3, esto es, una circunferencia de centro O y radio 3.
, los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es igual a 3, esto es, una circunferencia de centro O y radio 3.
- b) Como
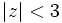 , los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es menor que 3, esto es, una círculo de centro O y radio 3 sin la circunferencia del borde.
, los números complejos que cumplen esa condición son los puntos del plano cuya distancia al origen es menor que 3, esto es, una círculo de centro O y radio 3 sin la circunferencia del borde.
- c) Como
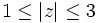 , la solución es una corona circular de radios 1 y 3 y centro O, incluidas las circunferencias de los bordes.
, la solución es una corona circular de radios 1 y 3 y centro O, incluidas las circunferencias de los bordes.
- d) Como
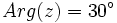 la solución es una semirrecta abierta de origen O que forma un ángulo de 30º con el eje X.
la solución es una semirrecta abierta de origen O que forma un ángulo de 30º con el eje X.
En esta escena de Geogebra podrás ver como se representan gráficamente las soluciones.
Ejercicios
Ejercicios propuestos
|
Ejercicios propuestos: Forma polar de un número complejo |
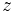 es la longitud del vector que lo representa, es decir, la distancia entre el afijo
es la longitud del vector que lo representa, es decir, la distancia entre el afijo 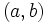 y el origen
y el origen 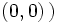 . Se designa por
. Se designa por 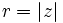 .
.
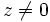 ), es el ángulo que forma el vector con el eje X . Se designa por
), es el ángulo que forma el vector con el eje X . Se designa por 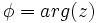 . De los infinitos argumentos de un número complejo, al comprendido entre 0º y 360º se le llama argumento principal.
. De los infinitos argumentos de un número complejo, al comprendido entre 0º y 360º se le llama argumento principal.
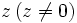 , se designa
, se designa 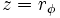 , entonces:
, entonces:
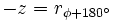
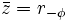
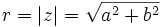
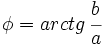
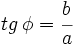 .
.
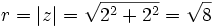
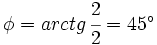
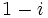 a forma polar.
a forma polar.
 se obtiene de la siguiente manera:
se obtiene de la siguiente manera: