Números complejos: Operaciones en forma polar (1ºBach)
De Wikipedia
| Revisión de 08:12 22 ene 2018 Coordinador (Discusión | contribuciones) (→División de números complejos en forma polar) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→División de números complejos en forma polar) |
||
| Línea 97: | Línea 97: | ||
| ==División de números complejos en forma polar== | ==División de números complejos en forma polar== | ||
| - | {{Teorema|titulo=División de complejos en forma polar|enunciado=La división de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos. | + | {{Teorema|titulo=División de complejos en forma polar|enunciado=La división de dos numeros complejos en forma polar, <math>r_\alpha\;</math> y <math>s_\beta \ , \ (s_\beta \ne 0)</math>, es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos. |
| {{Caja|contenido=<math>\cfrac{r_\alpha}{s_\beta}=\Big( \cfrac{r}{s} \, \Big)_{\alpha - \beta}</math>}} | {{Caja|contenido=<math>\cfrac{r_\alpha}{s_\beta}=\Big( \cfrac{r}{s} \, \Big)_{\alpha - \beta}</math>}} | ||
| + | |||
| + | |||
| |demo=En efecto: | |demo=En efecto: | ||
| :<math>\Big( \cfrac{r}{s} \, \Big)_{\alpha - \beta} \cdot s_\beta = \Big( \cfrac{r}{s} \cdot s \, \Big)_{\alpha - \beta + \beta} = r_\alpha</math> | :<math>\Big( \cfrac{r}{s} \, \Big)_{\alpha - \beta} \cdot s_\beta = \Big( \cfrac{r}{s} \cdot s \, \Big)_{\alpha - \beta + \beta} = r_\alpha</math> | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Multiplicación de números complejos en forma polar
Producto de complejos en forma polar
El producto de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el producto de los módulos y el argumento la suma de los argumentos de los respectivos complejos.
|
|
Expresando los complejos en forma trigonométrica:
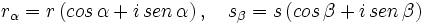
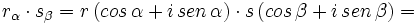
En esta escena podrás ver como se representan las multiplicaciones de números complejos en forma polar.
Videotutorial.
Potencias de números complejos en forma polar
Potencia de un complejo en forma polar
- La potencia n-ésima de un compejo se obtiene de la siguiente manera:
|
|
La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto:
En esta escena podrás ver como se representan las potencias de números complejos en forma polar.
Potencias sucesivas de la unidad imaginaria. Ejemplos.
3 ejercicios.
Fórmula de Moivre
Fórmula de Moivre
Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo:
Calcula 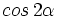 y
y 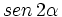 mediante la fórmula de Moivre.
mediante la fórmula de Moivre.
Solución:
Hay que hacer n=2 en la fórmula de Moivre, desarrollar el cuadrado de la izquierda, y después igualar las partes reales y las partes imaginarias en la igualdad.
División de números complejos en forma polar
División de complejos en forma polar
La división de dos numeros complejos en forma polar, 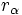 y
y 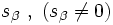 , es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos.
, es otro complejo en forma polar cuyo módulo es el cociente de los módulos y el argumento la diferencia de los argumentos de los respectivos complejos.
|
|
En efecto:
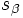 en ambos miembros, se obtiene la igualdad que queríamos demostrar.
en ambos miembros, se obtiene la igualdad que queríamos demostrar.En esta escena podrás ver como se representan las divisiones de números complejos en forma polar.
Videotutorial.
3 ejemplos.
Ejercicios propuestos
|
Ejercicios propuestos: Operaciones con complejos en forma polar |
Radicación de números complejos en forma polar
Un número complejo 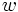 es una raíz n-ésima de otro complejo
es una raíz n-ésima de otro complejo 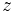 si se cumple que
si se cumple que 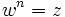 .
.
Raíces de un complejo
- Un número complejo
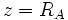 tiene exactamente n raíces n-ésimas
tiene exactamente n raíces n-ésimas 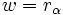 , que se obtienen de la siguiente manera:
, que se obtienen de la siguiente manera:
![r_\alpha : \begin{cases} r=\sqrt[n]{R} \\ \alpha=\cfrac{A+2k \pi}{n}\, , \quad k=0,1,\cdots,(n-1) \end{cases}](/wikipedia/images/math/4/a/5/4a5dd4f3f68e14f0c8013ccc27085e5e.png)
- Además, las n raíces están ubicadas en el plano complejo en los vértices de un polígono regular de n lados cuyo centro es el origen de coordenadas.
Por la definición de raíz n-ésima:
Igualando módulos ya rgumentos:
A partir de k=n, los ángulos que se obtienen son coterminales con los ya obtenidos.
Para la segunda parte, fíjate que todas las raíces tienen el mismo módulo, por lo que están a la misma distancia del origen, es decir, están en una circunferencia de centro el origen y radio ![r=\sqrt[n]{R}](/wikipedia/images/math/5/7/5/575ec5538dab079cec486d939b03cadc.png) .
.
En cuanto a los argumentos, tenemos que:
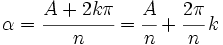
por lo que cada raíz se obtiene girando la anterior un mismo ángulo 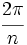 . Como este ángulo resulta de dividir en n partes iguales una vuelta completa de circunferencia, las n raíces están separadas entre sí por un mismo ángulo central.
. Como este ángulo resulta de dividir en n partes iguales una vuelta completa de circunferencia, las n raíces están separadas entre sí por un mismo ángulo central.
Calcula ![\sqrt[3]{1+i}](/wikipedia/images/math/8/8/3/883e0a5f87d5879d879d48e3bbe5789d.png)
Solución:
Primero pasamos el complejo 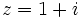 a forma polar:
a forma polar:
Así, 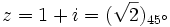
Ahora procedemos a calcular sus 3 raíces cubicas:
![\sqrt[3]{(\sqrt{2})_{45^\circ}}=r_\alpha](/wikipedia/images/math/c/5/e/c5e849c7713f59a373e993c0d21a8bd5.png) , siendo
, siendo ![\begin{cases} r=\sqrt[3]{\sqrt{2}} \\ \alpha=\cfrac{45^\circ +2k \pi}{3}\, , \quad k=0,1,2 \end{cases}](/wikipedia/images/math/e/3/3/e338be4b3b0010eb3dd1abb6ea6669f0.png)
De donde ![r_\alpha : \begin{cases} r=\sqrt[6]{2} \\ \alpha= 15^\circ \, , \quad 135^\circ \, , \quad 257^\circ \end{cases}](/wikipedia/images/math/d/9/7/d978739b21c71e554a372161eb06a8b7.png)
Soluciones:
En esta escena podrás ver como se representan las raíces de números complejos en forma polar.
Videotutorial.
2 ejercicios (Raíces sextas de -64 y de 64).
2 ejercicios (Raíces cúbicas de 1 y de -1).
2 ejercicios (Raíces cuartas de 1 y de -1).
Halla las raíces cúbicas de 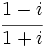 .
.
Halla las raíces cuartas de 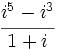 .
.
Los afijos de los números complejos  ,
, 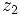 y
y 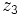 son los vértices de un triángulo equilátero inscrito en una circunferencia de centro el origen de coordenadas. Sabiendo que
son los vértices de un triángulo equilátero inscrito en una circunferencia de centro el origen de coordenadas. Sabiendo que 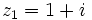 , calcula
, calcula 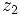 y
y 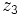 .
.
Ejercicios propuestos
|
Ejercicios propuestos: Raíces de números complejos |
Ejercicios y videotutoriales
Repaso de las operaciones con complejos en forma polar con ejemplos.
Multiplicaciones, divisiones y potencias de complejos en forma polar.
Sea 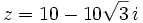 , calcula:
, calcula:
a) 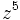
b) ![\sqrt[4]{z}](/wikipedia/images/math/9/3/f/93f257c77eb6dc38e437630b7937ac03.png)
Encuentra las ecuaciones de segundo grado cuyas raíces son:
a) 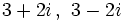
b) 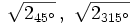
Resolución de ecuaciones con soluciones complejas.
El producto de dos números complejos es -8. Halla sus módulos y argumentos sabiendo que uno de ellos es el cuadrado del otro.
Calcula 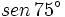 y
y 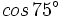 mediante el producto
mediante el producto 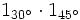
Halla dos números complejos tales que su cociente sea 3, la suma de sus argumentos 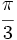 y la suma de sus módulos 8.
y la suma de sus módulos 8.
El producto e dos números complejos es 2i y el cubo de uno de ellos dividido por el otro es 1/2. Hállalos.
De dos números complejos sabemos que:
a) Tienen el mismo módulo.
b) Sus argumentos suman 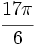 .
.
c) El primero es conjugado del cuadrado del segundo.
¿Cuáles son esos números?
Halla las coordenadas polares de los vértices, el perímetro y el área de un triángulo sabiendo que sus vértices son los afijos de ![\sqrt[3]{-6}](/wikipedia/images/math/8/c/b/8cb3155458419d36267bad202db41cdc.png) .
.
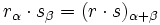
![=r \cdot s \, [cos \alpha \, \cos \beta + i \, cos \alpha \, sen \beta + i \, sen \, \alpha \, cos \, \beta + i^2 \, sen \, \alpha \, sen \, \beta ]=](/wikipedia/images/math/5/9/1/591804e8ee81496a02138c096a8d2d59.png)
![=r \cdot s \, [cos \alpha \, \cos \beta - sen \, \alpha \, sen \, \beta+ i \, ( cos \alpha \, sen \beta + sen \, \alpha \, cos \, \beta )]=](/wikipedia/images/math/2/f/c/2fcccb290acf0ed109301fe82ce33846.png)
![=r \cdot s \, [cos (\alpha + \beta ) + i \, sen \, ( \alpha + \beta )]=(r \cdot s)_{\alpha + \beta}](/wikipedia/images/math/7/6/d/76d54879d578a64886a5aeeafb79b32e.png)
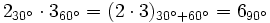
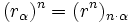
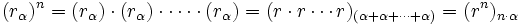
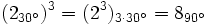
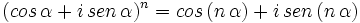
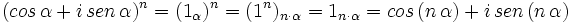
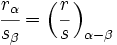
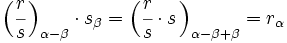
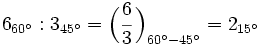
![\sqrt[n]{z}=w \iff z=w^n \iff (R_A)=(r_\alpha)^n \iff R_A=(r^n)_{n \, \alpha}](/wikipedia/images/math/b/7/7/b7781ba8724c717e4f2b2423267ad5bf.png)
![R_A=(r^n)_{n \, \alpha} \iff \begin{cases} r^n=R \iff r=\sqrt[n]{R} \\ n \, \alpha = A + 2k \pi \iff \alpha=\cfrac{A+2k \pi}{n}\, , \quad k=0,1,\cdots,(n-1) \end{cases}](/wikipedia/images/math/c/8/0/c808af8500c52fdd7279ea16c43c86cc.png)
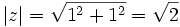
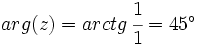
![(\sqrt[6]{2})_{15^\circ} \, , \quad (\sqrt[6]{2})_{135^\circ} \, , \quad (\sqrt[6]{2})_{257^\circ}](/wikipedia/images/math/a/d/b/adb33551ba73519cab6c3b98e938918b.png)