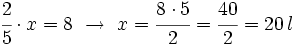Plantilla:La fracción como operador
De Wikipedia
| Revisión de 17:43 31 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para calcular la fracción de una cantidad, se divide la cantidad entre el denominador y se multiplica por el numerador. | + | Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos. |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | {{Teorema_sin_demo|titulo=Fracción de una cantidad|enunciado=Para calcular una fracción ''a/b'' de una cantidad ''C'' se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por ''C''). | ||
| - | {{Ejemplo|titulo=Ejercicio resuelto: ''La fracción como operador'' | + | <center><math>\cfrac{a}{b} \ \mbox{de} \ C = \cfrac{C}{b} \cdot a = \cfrac{a \cdot C}{b}= \cfrac{a}{b} \cdot C</math></center> |
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo 1: ''Cálculo de la parte conocido el total'' | ||
| |enunciado= | |enunciado= | ||
| Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito? | Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito? | ||
| Línea 14: | Línea 17: | ||
| {{p}} | {{p}} | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Actividades: ''La fracción como operador (problema directo)'' | + | |titulo1=Actividades: ''La fracción como operador'' |
| |descripcion=Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada. | |descripcion=Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena5/1q5_ejercicios_resueltos_4a.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena5/1q5_ejercicios_resueltos_4a.htm | ||
| Línea 23: | Línea 26: | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/03.htm | + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/07/03.htm |
| width=800 | width=800 | ||
| height=650 | height=650 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/07/03.htm | + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/07/03.htm |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo | {{Ejemplo | ||
| - | |titulo=Ejemplo: ''La fracción como operador (problema inverso)'' | + | |titulo=Ejemplo 2: ''Cálculo del total conocida la parte'' |
| |enunciado=Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito? | |enunciado=Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito? | ||
| |sol= | |sol= | ||
Revisión actual
Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos.
Fracción de una cantidad
Para calcular una fracción a/b de una cantidad C se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por C).
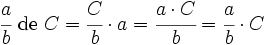
Ejemplo 1: Cálculo de la parte conocido el total
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada.
Ejemplo 2: Cálculo del total conocida la parte
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?
La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
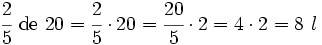
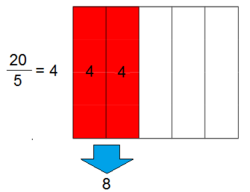
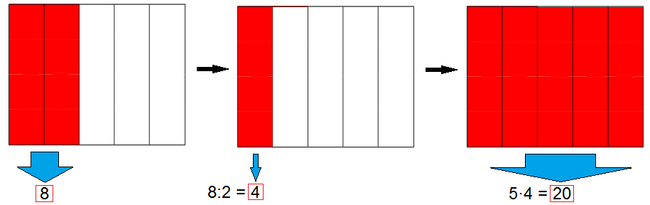
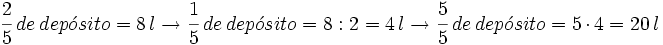
 = capacidad del depósito.
= capacidad del depósito.