Plantilla:Relación de proporcionalidad directa 1ºESO
De Wikipedia
| Revisión de 16:04 17 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{AI_anaya | {{AI_anaya | ||
| - | |titulo1=Cálculo del valor de varios a partir del valor de uno | + | |titulo1=Actividad |
| - | |descripcion= | + | |descripcion=Cálculo del valor de varios a partir del valor de uno |
| - | + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/09/01.htm | |
| - | <center><iframe> | + | }} |
| - | url=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/09/01.htm | + | {{p}} |
| - | width=800 | + | {{Caja_Amarilla|texto=Dos [[El Sistema Métrico Decimal (1º ESO)|magnitudes]] son '''directamente proporcionales''' cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda multiplicada (resp. dividida) por el mismo número. |
| - | height=650 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | |url1=http://web.educastur.princast.es/ies/pravia/carpetas/recursos/mates/anaya1/datos/09/01.htm | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=Dos magnitudes son '''directamente proporcionales''' cuando al multiplicar (resp. dividir) una de ellas por un número, la otra queda multiplicada (resp. dividida) por el mismo número. | + | {{Warning|titulo=Advertencia|texto=Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar (resp. disminuir) una de ellas, aumenta (resp. disminuye) la otra. No es exactamente así. No es suficiente con que aumente (resp. disminuya) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se multiplica (resp. divide) la otra, por el mismo número. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 54: | Línea 49: | ||
| |sinopsis=Magnitudes directamente proporcionales. Ejemplos. | |sinopsis=Magnitudes directamente proporcionales. Ejemplos. | ||
| |url1=https://www.youtube.com/watch?v=HeM1h-KLJng | |url1=https://www.youtube.com/watch?v=HeM1h-KLJng | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Tutorial 3 | ||
| + | |duracion=4'31" | ||
| + | |sinopsis=Relaciones directamente proporcionales. Ejemplo. | ||
| + | |||
| + | '''Aviso:''' En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales". | ||
| + | |url1=https://www.youtube.com/watch?v=uDnwqQmChqk | ||
| + | }} | ||
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 1 | ||
| + | |duracion=3'01" | ||
| + | |sinopsis=Hoy Nate tiene 100 plátanos. Él va a comer 2 plátanos de ellos cada día. | ||
| + | |||
| + | :a) ¿El número de plátanos que Nate deja sin comer es directamente proporcional al número de días transcurridos? | ||
| + | :b) ¿Y el número de plátanos que come cada día? | ||
| + | |||
| + | '''Aviso:''' En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales". | ||
| + | |url1=https://www.youtube.com/watch?v=jdweZXjY3Ik | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio 2 | ||
| + | |duracion=1'56" | ||
| + | |sinopsis=Un cine cobra $10.50 por boleto y $5 por bolsa de palomitas. Tú nunca compras las palomitas porque te parece que son muy caras. ¿El precio total de lo que pagas es directamente proporcional al número de boletos que compras? | ||
| + | |||
| + | '''Aviso:''' En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales". | ||
| + | |url1=https://www.youtube.com/watch?v=jhBJVMAkrQo | ||
| }} | }} | ||
| }} | }} | ||
| Línea 69: | Línea 92: | ||
| {{AI_anaya | {{AI_anaya | ||
| |titulo1=Actividad 2 | |titulo1=Actividad 2 | ||
| - | |descripcion= | + | |descripcion=Completa las tablas de manera que las magnitudes sean directamente proporcionales. |
| - | <center><iframe> | + | |
| - | url=http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud09/1/01.htm | + | |
| - | width=800 | + | |
| - | height=650 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| |url1=http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud09/1/01.htm | |url1=http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud09/1/01.htm | ||
| }} | }} | ||
| Línea 88: | Línea 105: | ||
| |enlace=[http://www.geogebra.org/m/b2nS96n8 Autoevaluación 1] | |enlace=[http://www.geogebra.org/m/b2nS96n8 Autoevaluación 1] | ||
| }} | }} | ||
| - | {{AI_vitutor | + | {{AI_Khan |
| |titulo1=Autoevaluación 2 | |titulo1=Autoevaluación 2 | ||
| + | |descripcion=Ejercicios de autoevaluación sobre magnitudes directamente proporcionales. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-ratios-rates/pre-algebra-proportional-rel/e/analyzing-and-identifying-proportional-relationships | ||
| + | }} | ||
| + | {{AI_vitutor | ||
| + | |titulo1=Autoevaluación 3 | ||
| |descripcion=Ejercicios de autoevaluación sobre magnitudes directamente proporcionales. | |descripcion=Ejercicios de autoevaluación sobre magnitudes directamente proporcionales. | ||
| |url1=http://www.vitutor.com/di/p/a_4e.html | |url1=http://www.vitutor.com/di/p/a_4e.html | ||
| Línea 96: | Línea 118: | ||
| {{p}} | {{p}} | ||
| ===Constante de proporcionalidad directa=== | ===Constante de proporcionalidad directa=== | ||
| - | {{Teorema_sin_demo|titulo=Constante de proporcionalidad|enunciado=Al dividir dos magnitudes directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama '''constante o razón de proporcionalidad'''.}} | + | {{Caja_Amarilla|texto=Al dividir dos [[El Sistema Métrico Decimal (1º ESO)|magnitudes]] directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama '''constante o razón de proporcionalidad'''.}} |
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| Línea 131: | Línea 153: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_angelmartinez | {{Video_enlace_angelmartinez | ||
| - | |titulo1=Razón de proporcionalidad directa | + | |titulo1=Constante de proporcionalidad directa |
| |duracion=0'44" | |duracion=0'44" | ||
| |sinopsis=Razón de proporcionalidad directa. Ejemplo. | |sinopsis=Razón de proporcionalidad directa. Ejemplo. | ||
| |url1=https://www.youtube.com/watch?v=15DXlMLF4y8 | |url1=https://www.youtube.com/watch?v=15DXlMLF4y8 | ||
| }} | }} | ||
| + | {{Actividades|titulo=Constante de proporcionalidad directa|enunciado= | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Constante de proporcionalidad directa | + | |titulo1=Constante de proporcionalidad directa (I) |
| |descripcion=Actividades para aprender a calcular la constante de proporcionalidad directa. | |descripcion=Actividades para aprender a calcular la constante de proporcionalidad directa. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena6/1quincena6_contenidos_2b.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena6/1quincena6_contenidos_2b.htm | ||
| + | }} | ||
| + | {{AI_cidead | ||
| + | |titulo1=Constante de proporcionalidad directa (II) | ||
| + | |descripcion=Actividades para aprender a calcular la constante de proporcionalidad directa. | ||
| + | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena4/2quincena4_contenidos_2a.htm | ||
| }} | }} | ||
| {{AI_enlace | {{AI_enlace | ||
| Línea 146: | Línea 174: | ||
| |descripcion=Halla la constante de proporcionalidad. | |descripcion=Halla la constante de proporcionalidad. | ||
| - | |url1=https://scratch.mit.edu/projects/embed/142211603/ | + | |url1=http://scratch.mit.edu/projects/embed/142211603/ |
| + | }} | ||
| }} | }} | ||
Revisión actual
Actividad Descripción: Cálculo del valor de varios a partir del valor de uno
Dos magnitudes son directamente proporcionales cuando al multiplicar (resp. dividir) una de ellas por un número distinto de cero, la otra queda multiplicada (resp. dividida) por el mismo número.
Es muy común pensar que dos magnitudes son directamente proporcionales si al aumentar (resp. disminuir) una de ellas, aumenta (resp. disminuye) la otra. No es exactamente así. No es suficiente con que aumente (resp. disminuya) la otra magnitud, tiene que hacerlo de una forma muy concreta: Si multiplicamos (resp. dividimos) una, se multiplica (resp. divide) la otra, por el mismo número.
La capacidad de un depósito de agua y el tiempo que tarda en llenarse son magnitudes directamente proporcionales, ya que si el depósito tiene el doble (o el triple,...) de capacidad, el tiempo que tarda en llenarse es el doble (o el triple,...).
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
Tutorial 1 (1'00") Sinopsis: Magnitudes directamente proporcionales. Ejemplo.
Tutorial 2 (4'16") Sinopsis:Magnitudes directamente proporcionales. Ejemplos.
Tutorial 3 (4'31") Sinopsis: Relaciones directamente proporcionales. Ejemplo.
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Ejercicio 1 (3'01") Sinopsis: Hoy Nate tiene 100 plátanos. Él va a comer 2 plátanos de ellos cada día.
- a) ¿El número de plátanos que Nate deja sin comer es directamente proporcional al número de días transcurridos?
- b) ¿Y el número de plátanos que come cada día?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Ejercicio 2 (1'56") Sinopsis: Un cine cobra $10.50 por boleto y $5 por bolsa de palomitas. Tú nunca compras las palomitas porque te parece que son muy caras. ¿El precio total de lo que pagas es directamente proporcional al número de boletos que compras?
Aviso: En este video llama "relaciones proporcionales" a lo que entendemos por "relaciones directamente proporcionales".
Magnitudes directamente proporcionales Descripción: Actividades para aprender que son magnitudes directamente proporcionales.
Actividad 1 Descripción: Actividades sobre magnitudes directamente proporcionales.
Actividad 2 Descripción: Completa las tablas de manera que las magnitudes sean directamente proporcionales.
Actividad 3 Descripción: Actividades sobre magnitudes directamente proporcionales.
Autoevaluación 1 Descripción: Actividad sobre magnitudes directamente proporcionales.
Autoevaluación 2 Descripción: Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Autoevaluación 3 Descripción: Ejercicios de autoevaluación sobre magnitudes directamente proporcionales.
Constante de proporcionalidad directa
Al dividir dos magnitudes directamente proporcionales siempre se obtiene el mismo valor. A dicho valor se le llama constante o razón de proporcionalidad.
En el ejemplo anterior, en el que relacionabamos la capacidad de un depósito con el tiempo que tardaba en llenarse
Capacidad (litros) |
100 |
200 |
300 |
400 |
500 |
Tiempo (min) |
5 |
10 |
15 |
20 |
25 |
se observa que:
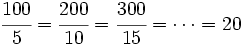
La constante de proporcinalidad es 20.
Constante de proporcionalidad directa (0'44") Sinopsis: Razón de proporcionalidad directa. Ejemplo.
Constante de proporcionalidad directa (I) Descripción: Actividades para aprender a calcular la constante de proporcionalidad directa.
Constante de proporcionalidad directa (II) Descripción: Actividades para aprender a calcular la constante de proporcionalidad directa.
Ejercicio Descripción: Halla la constante de proporcionalidad.
