Plantilla:Relación entre ángulos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:30 4 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Tabla75|celda2=<center>[[Imagen:angulos_consec.png|200px]]{{p}}Ángulos consecutivos.</center> | + | {{Tabla75|celda2={{p}}[[Imagen:angulos_consec.png|200px|center]]<br><center>Ángulos consecutivos</center><br>{{p}}<br>[[Imagen:angulos_opuestos_vertice.png|200px|center]]<center>'''a''' y '''c''' son opuestos por el vértice,{{p}}al igual que '''b''' y '''d'''</center> |
| |celda1= | |celda1= | ||
| {{Caja_Amarilla|texto=*Dos ángulos son '''iguales''' si tienen la misma amplitud. | {{Caja_Amarilla|texto=*Dos ángulos son '''iguales''' si tienen la misma amplitud. | ||
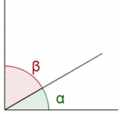
| - | *Dos ángulos son '''consecutivos''' si tienen el vértice y un lado en común.}} | + | * Ángulos '''complementarios''' son aquellos cuya suma es un ángulo recto. |
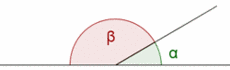
| + | * Ángulos '''suplementarios''' son aquellos cuya suma es un ángulo llano. | ||
| + | * Ángulos '''conjugados''' son aquellos cuya suma es un ángulo completo. | ||
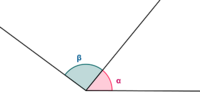
| + | *Dos ángulos son '''consecutivos''' si tienen el vértice y un lado en común. | ||
| + | *Dos ángulos son '''adyacentes''' si tienen el vértice y un lado en común, al tiempo que sus otros dos lados son semirrectas opuestas. Por tanto son consecutivos y suplementarios simultáneamente. | ||
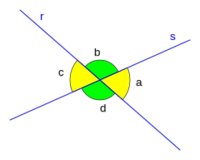
| + | * Ángulos '''opuestos por el vértice '''son aquellos que cumplen que los lados de uno son semirrectas opuestas a los lados del otro. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto= | + | <br> |
| - | * Ángulos '''complementarios '''son aquellos cuya suma es un ángulo recto. | + | {{Tabla50|celda1=[[Imagen:angulos_complementarios.gif|120px|center]]{{p}}<center>Ángulos complementarios</center> |
| - | {{p}} | + | |celda2=<br><br>[[Imagen:angulos_suplementarios.gif|230px|center]]{{p}}<center>Ángulos suplementarios</center> |
| - | * Ángulos '''suplementarios '''son aquellos cuya suma es un ángulo llano. | + | }} |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Tabla50|celda1=[[Imagen:angulos_complementarios.gif|120px|center]]{{p}}<center>Ángulos complementarios</center> | + | {{Videotutoriales|titulo=Relaciones entre ángulos|enunciado= |
| - | |celda2=<br><br>[[Imagen:angulos_suplementarios.gif|230px|center]]{{p}}<center>Ángulos complementarios</center>}} | + | {{Video_enlace_sensei |
| - | {{p}} | + | |titulo1=Tutorial 1 |
| + | |duracion=3'33" | ||
| + | |url1=https://www.youtube.com/watch?v=tjSljSa9cYY | ||
| + | |sinopsis=Ángulos complementarios, suplementarios, opuestos por el vértice y formados por rectas secantes. | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=4´36" | ||
| + | |url1=https://www.youtube.com/watch?v=-KR_Jp6IlRU | ||
| + | |sinopsis=Con este video vamos a estudiar la clasificación de los ángulos de acuerdo a su relación: ángulos consecutivos, ángulos complementarios, ángulos suplementarios, ángulos conjugados, ángulos opuestos por el vértice y ángulos adyacentes. | ||
| + | }} | ||
| {{Video_enlace_abel | {{Video_enlace_abel | ||
| - | |titulo1=Ángulos complementarios y suplementarios | + | |titulo1=Tutorial 3 |
| |duracion=9´19" | |duracion=9´19" | ||
| |url1=https://www.youtube.com/watch?v=4jwsRibeE6k | |url1=https://www.youtube.com/watch?v=4jwsRibeE6k | ||
| |sinopsis=Ángulos complementarios y suplementarios. Ejemplos. | |sinopsis=Ángulos complementarios y suplementarios. Ejemplos. | ||
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace_escuela |
| - | {{Tabla75|celda2=[[Imagen:angulos_opuestos_vertice.png|200px|center]] | + | |titulo1=Tutorial 4 |
| - | |celda1= | + | |duracion=5'55" |
| - | {{Caja_Amarilla|texto= | + | |sinopsis=Ángulos relacionados según su posición y según su amplitud. |
| - | * Ángulos '''opuestos por el vértice '''son aquellos que cumplen que los lados de uno son semirrectas opuestas a los lados del otro. | + | |url1=https://www.youtube.com/watch?v=QQuTGYTsNWQ&list=PLw7Z_p6_h3ow5KgdlUWDX7Lcu4w0guR1Y&index=5 |
| }} | }} | ||
| - | {{p}} | + | {{Video_enlace |
| - | En la imagen de la derecha, '''a''' y '''c''' son opuestos por el vértice, al igual que '''b''' y '''d'''. | + | |titulo1=Tutorial 5 |
| - | {{p}} | + | |duracion=5´43" |
| - | {{Geogebra_enlace | + | |url1=https://www.youtube.com/watch?v=pdJ7ZLPfJHE |
| - | |descripcion=En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice. | + | |sinopsis=Ángulos consecutivos, complementarios, suplementarios y adyacentes. |
| - | |enlace=[https://ggbm.at/WSw5AKar Ángulos complementarios, suplementarios y opuestos por el vértice] | + | |
| }} | }} | ||
| + | }} | ||
| + | {{Actividades|titulo=Relaciones entre ángulos|enunciado= | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Relaciones entre ángulos | + | |titulo1=Actividad 1 |
| |descripcion=Actividad en la que podrás observar las distintas relaciones que hay entre ángulos. | |descripcion=Actividad en la que podrás observar las distintas relaciones que hay entre ángulos. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_3c.htm | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_3c.htm | ||
| + | }} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice. | ||
| + | |enlace=[https://ggbm.at/WSw5AKar Actividad 2] | ||
| + | }} | ||
| + | {{AI_anaya | ||
| + | |titulo1=Actividad 3 | ||
| + | |descripcion= | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/11/02.htm | ||
| + | width=800 | ||
| + | height=650 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/11/02.htm | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
|  Ángulos consecutivos
 |
Tutorial 1 (3'33") Sinopsis:Ángulos complementarios, suplementarios, opuestos por el vértice y formados por rectas secantes.
Tutorial 2 (4´36") Sinopsis: Con este video vamos a estudiar la clasificación de los ángulos de acuerdo a su relación: ángulos consecutivos, ángulos complementarios, ángulos suplementarios, ángulos conjugados, ángulos opuestos por el vértice y ángulos adyacentes.
Tutorial 3 (9´19") Sinopsis:Ángulos complementarios y suplementarios. Ejemplos.
Tutorial 4 (5'55") Sinopsis: Ángulos relacionados según su posición y según su amplitud.
Tutorial 5 (5´43") Sinopsis:Ángulos consecutivos, complementarios, suplementarios y adyacentes.
Actividad 1 Descripción: Actividad en la que podrás observar las distintas relaciones que hay entre ángulos.
Actividad 2 Descripción: En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice.
Actividad 3 Descripción: 
