Plantilla:Construccion otras raices

(Diferencia entre revisiones)

Revisión actual

Representación de otras raíces cuadradas Descripción:

Observa en la escena la representación de otras raices cuadradas.

Pulsando sobre el control pasos puedes observar cómo se representa la raíz cuadrada de cualquier número entero.
Representa en tu cuaderno la raíz de 3 y la raíz de 5.
Pulsando el control decimales puedes obtener el número de ellos que desees.
Utiliza el botón Limpiar si quieres ver con más claridad la representación de algún número.

Representación de raíces cuadradas Descripción:

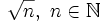En esta escena podrás ver como se representan gráficamente los números del tipo $\sqrt{n},~n \in \mathbb{N}$ .

Representación gráfica de raíces cuadradas Descripción:

En esta escena podrás ver como se representan gráficamente algunas raíces cuadradas.

-{{AI_cidead
-|titulo1=Representación gráfica de otrass raíces cuadradas
-|descripción=Observa en la escena la representación de otras raíces cuadradas.
-|url1=http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/reales/quincena1_contenidos_1e.htm
-}}
 {{AI_descartes
 |titulo1=Representación de otras raíces cuadradas
 |descripcion=En esta escena podrás ver como se representan gráficamente los números del tipo <math>\sqrt{n},~n \in \mathbb{N}</math>.
 |enlace=[http://ggbm.at/tEx3VB9x Representación de raíces cuadradas]
+}}
+{{AI_cidead
+|titulo1=Representación gráfica de raíces cuadradas
+|descripcion=En esta escena podrás ver como se representan gráficamente algunas raíces cuadradas.
+|url1=http://recursostic.educacion.es/secundaria/edad/4esomatematicasB/reales/quincena1_contenidos_1e.htm
 }}