Plantilla:La recta real
De Wikipedia
| Revisión de 19:37 23 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 15: | Línea 15: | ||
| |sinopsis=El conjunto de los números reales es la unión del conjunto de los números racionales (tienen un número finito de decimales o son periódicos) y del conjunto de los números irracionales (tienen infinitos decimales y no son periódicos). | |sinopsis=El conjunto de los números reales es la unión del conjunto de los números racionales (tienen un número finito de decimales o son periódicos) y del conjunto de los números irracionales (tienen infinitos decimales y no son periódicos). | ||
| La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto". | La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto". | ||
| - | |url1=https://www.youtube.com/watch?v=GRsEFF95Zfk | + | |url1=http://www.youtube.com/watch?v=GRsEFF95Zfk |
| + | }} | ||
| + | {{p}} | ||
| + | {{AI_descartes | ||
| + | |titulo1=Actividad: ''La recta real''|cuerpo= | ||
| + | |||
| + | |descripcion=Los números reales en la recta real. | ||
| + | {{p}} | ||
| + | Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas. | ||
| + | |||
| + | Luego introduce distintos número y observa su representación en la recta real: | ||
| + | #Introduce las fracciones <math>\cfrac{5}{3}, \cfrac{1}{7}, \cfrac{5}{4}, -\cfrac{23}{3} </math> (teclea a/b para introducir la fracción <math>\cfrac{a}{b}</math>) | ||
| + | #Introduce la raíz cuadrada de 2, 5, 7, 11 (teclea sqrt(n) para introducir la raíz cuadrada de n) | ||
| + | {{p}} | ||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros5_1.html | ||
| + | width=500 | ||
| + | height=200 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |url1=http://maralboran.org/web_ma/descartes/3_eso/Numeros_Reales_Aproximaciones/numeros5_1.html | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 33: | Línea 53: | ||
| '''Recta real ampliada:''' conjunto que resulta al añadir los símbolos +∞ y -∞ al conjunto de los reales. | '''Recta real ampliada:''' conjunto que resulta al añadir los símbolos +∞ y -∞ al conjunto de los reales. | ||
| Que quede muy claro: +∞ y -∞ no son números, y para todo real "x" es -∞ < x < +∞. | Que quede muy claro: +∞ y -∞ no son números, y para todo real "x" es -∞ < x < +∞. | ||
| - | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/06-la-recta-real-ampliada-6#.VCVYdRZ8HA8}} | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/01-funciones-reales-de-una-variable-real-2/06-la-recta-real-ampliada-6#.VCVYdRZ8HA8 |
| + | }} | ||
Revisión actual
La recta real es una representación geométrica del conjunto de los números reales.
Para su construcción:
- Se elige un punto de referencia arbitrario sobre la recta al que se denomina origen y al que se le asocia el número 0.
- Se selecciona una unidad U de longitud para medir distancias que es la que separa los números 0 y 1.
- Se elige también un sentido a lo largo de la recta a la que se llama positivo y se considera como negativo al sentido opuesto.
- A cada número real p se le asocia un punto de la recta que está a una distancia de p unidades del origen en la dirección positiva o negativa, dependiendo de si el número p es positivo o negativo, respectivamente.
Los números reales. La recta real (16´23") Sinopsis: El conjunto de los números reales es la unión del conjunto de los números racionales (tienen un número finito de decimales o son periódicos) y del conjunto de los números irracionales (tienen infinitos decimales y no son periódicos). La "visualización" del conjunto de los números reales es la llamada "recta real": a cada número real le corresponde un único "punto" de la "recta real" y viceversa: cada "punto" de la recta real corresponde a un único número real. Por eso, consideraremos sinónimas las palabras "número" y "punto".
Actividad: La recta real Descripción: Los números reales en la recta real.
Mueve el punto rojo y observa que todo punto de la recta representa un número real. Utiliza el zoom para ampliar la vista, si lo deseas.
Luego introduce distintos número y observa su representación en la recta real:
- Introduce las fracciones
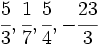(teclea a/b para introducir la fracción 
)
- Introduce la raíz cuadrada de 2, 5, 7, 11 (teclea sqrt(n) para introducir la raíz cuadrada de n)
Densidad de los números racionales e irracionales
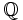es denso en 
: Entre cada dos números reales existe un racional, y por tanto hay infnitos.
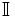es denso en : Entre cada dos números reales existe un irracional, y por tanto hay infnitos.
Completitud de los números reales
Gracias al axioma del supremo o axioma de completitud, el conjunto de los números reales cubre o completa la recta sin dejar "huecos". Existe una correspondencia biunívoca entre los puntos de la recta y los números reales de manera que a cada punto de la recta le hace corresponder un único número real y viceversa.
La recta real ampliada (8'14") Sinopsis: Este video te servirá en el tema de límites para manipular mejor expresiones con límites infinitos.
Recta real ampliada: conjunto que resulta al añadir los símbolos +∞ y -∞ al conjunto de los reales. Que quede muy claro: +∞ y -∞ no son números, y para todo real "x" es -∞ < x < +∞.
