Plantilla:Teorema del resto
De Wikipedia
| Revisión de 18:56 29 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:37 15 sep 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| |enunciado=Calcula el resto de dividir el polinomio <math>x^3 - 3x^2 - 7\;</math> entre <math>(x-2)\;</math> | |enunciado=Calcula el resto de dividir el polinomio <math>x^3 - 3x^2 - 7\;</math> entre <math>(x-2)\;</math> | ||
| |sol= | |sol= | ||
| + | '''Primer método:''' | ||
| + | |||
| Bastará calcular <math>P(2)=2^3-3 \cdot 2^2-7=-11</math> | Bastará calcular <math>P(2)=2^3-3 \cdot 2^2-7=-11</math> | ||
| Así el resto será <math>r=P(2)=-11\;</math> | Así el resto será <math>r=P(2)=-11\;</math> | ||
| + | ---- | ||
| + | '''Segundo método:''' | ||
| + | |||
| + | Usando la regla de Ruffini: | ||
| + | |||
| + | <pre> | ||
| + | | 1 -3 0 -7 | ||
| + | | | ||
| + | 2| 2 -2 -4 | ||
| + | --|---------------- | ||
| + | | 1 -1 -2 |-11 | ||
| + | |____ | ||
| + | </pre> | ||
| + | |||
| + | Así, el resto de la división es -11, y por el teorema del resto, P(2) = -11. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 17:37 15 sep 2018
Teorema del Resto
El valor que toma un polinomio,  , cuando hacemos
, cuando hacemos  , coincide con el resto de la división de
, coincide con el resto de la división de  entre
entre 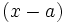 . Es decir,
. Es decir, 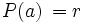 , donde
, donde  es el resto de dicha división.
es el resto de dicha división.
Esto se deduce directamente de una de las propiedades de la división, la que dice que:
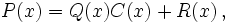
donde  es el dividendo,
es el dividendo,  el divisor,
el divisor, 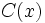 el cociente y
el cociente y 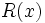 el resto y verificándose además, que el grado de
el resto y verificándose además, que el grado de 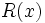 es menor que el grado de
es menor que el grado de  .
.
En efecto, si tomamos el divisor 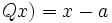 , entonces
, entonces 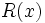 tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar
tiene grado menor que 1 (el grado del resto es 0); es decir, es una constante que podemos llamar  , y la fórmula anterior se convierte en:
, y la fórmula anterior se convierte en:
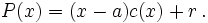
Tomando el valor 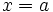 se obtiene que:
se obtiene que:
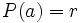
Ejemplo: Teorema del Resto
Calcula el resto de dividir el polinomio 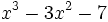 entre
entre 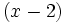
Primer método:
Bastará calcular 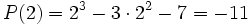
Así el resto será 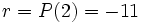
Segundo método:
Usando la regla de Ruffini:
| 1 -3 0 -7
|
2| 2 -2 -4
--|----------------
| 1 -1 -2 |-11
|____
Así, el resto de la división es -11, y por el teorema del resto, P(2) = -11.Si P(x) es un polinomio de grado no inferior a 1, el resto de la división P(x)/(x-a) es el número P(a) que se obtiene al sustituir "x" por "a" en P(x). La división P(x)/(x-a) es "exacta" si P(a) = 0; y en tal caso se dice que "a" es un "cero" o "raíz" del polinomio P(x), o una solución de la ecuación P(x) = 0.
- Teorema del resto para la división de un polinomio entre un binomio del tipo (ax+b).
- Como ejemplo, también resolveremos los siguientes ejercicios:
- 1) Halla el resto de dividir el polinomio
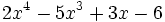 entre el binomio
entre el binomio 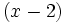 .
.
- 2) Halla el resto de dividir el polinomio
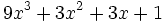 entre el binomio
entre el binomio 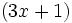 .
.
Halla el resto de la división del polinomio 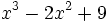 entre
entre 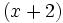 .
.
Halla el valor de  para que la división del polinomio
para que la división del polinomio 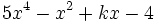 entre
entre 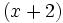 sea exacta.
sea exacta.
1) Halla el resto de la división del polinomio 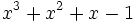 entre
entre 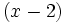 ,
, 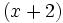 ,
, 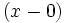 y
y 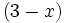 .
.
2) Determina el valor de k para que el polinomio 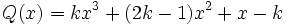 sea divisible por
sea divisible por 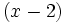 .
.
3) Sea 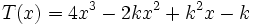 . Halla el valor de k para que el resto de la división de
. Halla el valor de k para que el resto de la división de 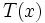 entre
entre 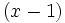 sea igual a 2.
sea igual a 2.
a) Halla el resto de la división de 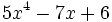 entre
entre 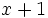 .
.
b) y c) Otros dos ejercicios de nivel superior.
Ejercicios de autoevaluación sobre el teorema del resto.

